Question

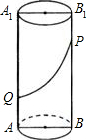附加题：有一圆柱体高为10 cm，底面圆的半径为4 cm，AA₁、BB₁为相对的两条母线，在AA₁上有一个蜘蛛Q，QA=3 cm；在BB₁上有一只苍蝇P，PB₁=2 cm，蜘蛛沿圆柱体侧面爬到P点吃苍蝇，求最短路径．
（答案保留两个有效数字）

Answer 1

分析：要求不在同一个平面内的两点之间的最短距离，首先要把两个点展开到一个平面内，然后分析展开图形中的数据，根据勾股定理即可求解．

解答：解：将曲面沿AA₁展开，如图所示，过P作PM⊥AA₁于M，
在Rt△PQM中，∠PMQ=90°，MQ=10-2-3=5（cm），MP=

1

2

×2π×4=12，56（cm），
由勾股定理，得PQ=

MQ2+MP2

=

52+12.562

=13.52≈14（cm）．
答：蜘蛛所走的最短路线约是14cm．

点评：由于蜘蛛与苍绳均属于玻璃容器的外侧，因而蜘蛛不能直接到达点P，需沿侧面爬行．为此，可将曲面沿AA₁展开，显然蜘蛛所走的最短的路线即为线段PQ，从而可构造直角三角形，用勾股定理求出PQ的长．