Question

【题目】如图，在一斜坡坡顶处的同一水平线上有一古塔，为测量塔高，数学老师带领同学在坡脚处测得斜坡的坡角为，且，塔顶处的仰角为，他们沿着斜坡攀行了米，到达坡顶处，在处测得塔顶的仰角为．

（1）求斜坡的高度；

（2）求塔高．

Answer 1

【答案】(1)14米；（2）塔的高度为米．

【解析】

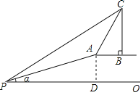
（1）在Rt△APD中，根据tanα的值设AD=7k，PD=24k，利用勾股定理表示出AP，根据AP=50，求出k的值，继而可求得AD的长度；
（2）延长CB交PO于点E，设塔高为x，在Rt△CBA中，求出AB的长度，然后在Rt△PCE中，根据∠CPE=30°，利用三角函数求解．

（1）在Rt△APD中，
∵tanα= ，
∴设AD=7k，PD=24k，
∴PA= =25k，
∵PA=50，
∴AD=APsinα=50×=14（m）；
（2）延长CB交PO于点E，可得四边形ABED为矩形，

设塔高为x，
在Rt△CBA中，
∵∠CAB=60°，tan60°= ，
∴AB= ，

在Rt△CPE中，
∵∠CPE=30°，
∴=tan30°，
即 ，
解得：x=24-21.

答：塔的高度为米.