题目内容
24、同学们，你已经熟悉完全平方公式：（a+b）2=a2+2ab+b2，当a＞0，b＞0时，完全平方公式可以用图（1）来说明．请你对图（2）进行适当的分割，猜想出（a+b+c）2的展开形式，并给出其推导过程．分析：本题考查的是完全平方公式的应用，公式中的a和b既可以是单项式也可以是多项式，因此有：（a+b+c）2=[（a+b）+c]2=（a+b）2+2c（a+b）+c2=a2+b2+c2+2ab+2ac+2bc．
解答：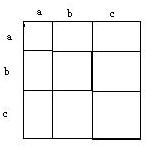
解：如图：
整体看大正方形的面积为：（a+b+c）2；
而大正方形是由三个小正方形和六个矩形组成，面积为：a2+b2+c2+2ab+2ac+2bc；
故有：（a+b+c）2=[（a+b）+c]2=（a+b）2+2c（a+b）+c2=a2+b2+c2+2ab+2ac+2bc．
解：如图：整体看大正方形的面积为：（a+b+c）2；
而大正方形是由三个小正方形和六个矩形组成，面积为：a2+b2+c2+2ab+2ac+2bc；
故有：（a+b+c）2=[（a+b）+c]2=（a+b）2+2c（a+b）+c2=a2+b2+c2+2ab+2ac+2bc．
点评：本题考查完全平方公式的应用，在应用公式时要分清什么是公式中的a和b．
练习册系列答案
黎明文化寒假作业系列答案
相关题目