题目内容
 如图,抛物的图象如图.
如图,抛物的图象如图.
(1)求抛物线的解析式;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标.
解:(1)设抛物线解析式为y=ax2+bx+c,
由图可知点A(-4,0),B(2,0),C(0,3),
所以, ,
,
解得 ,
,
所以,抛物线的解析式为y=- x2-
x2- x+3;
x+3;
(2)抛物线的对称轴为直线x=-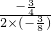 =-1,
=-1,
设直线AC与对称轴的交点为E,易求直线AC的解析式为y= x+3,
x+3,
x=-1时,y=- +3=
+3= ,
,
AB=2-(-4)=6,OC=3,
△ACB的面积= ×6×3=9,
×6×3=9,
△ACD的面积= DE•4=9,
DE•4=9,
解得DE= ,
,
点D在点E的上方时,点D的纵坐标为 +
+ =
= ,
,
点D在点E的下方时,点D的纵坐标为 -
- =-
=- ,
,
所以,点D的坐标为(-1, )或(-1,
)或(-1, ).
).
分析:(1)设抛物线解析式为y=ax2+bx+c,然后利用待定系数法求二次函数解析式即可;
(2)先根据抛物线的解析式求出对称轴解析式,设直线AC与对称轴的交点为E,先求出直线AC的解析式,再取出点E的坐标,然后求出△ACB的面积,再根据三角形的面积求出DE的长度,然后分点D在点E的上方与下方两种情况写出点D的坐标即可.
点评:本题考查了待定系数法求二次函数解析式,二次函数的性质,难点在于要分点D在AC的上方与下方两种情况讨论.
由图可知点A(-4,0),B(2,0),C(0,3),
所以,
 ,
,解得
 ,
,
所以,抛物线的解析式为y=-
 x2-
x2- x+3;
x+3;(2)抛物线的对称轴为直线x=-
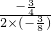 =-1,
=-1,设直线AC与对称轴的交点为E,易求直线AC的解析式为y=
 x+3,
x+3,x=-1时,y=-
 +3=
+3= ,
,AB=2-(-4)=6,OC=3,
△ACB的面积=
 ×6×3=9,
×6×3=9,△ACD的面积=
 DE•4=9,
DE•4=9,解得DE=
 ,
,点D在点E的上方时,点D的纵坐标为
 +
+ =
= ,
,点D在点E的下方时,点D的纵坐标为
 -
- =-
=- ,
,所以,点D的坐标为(-1,
 )或(-1,
)或(-1, ).
).分析:(1)设抛物线解析式为y=ax2+bx+c,然后利用待定系数法求二次函数解析式即可;
(2)先根据抛物线的解析式求出对称轴解析式,设直线AC与对称轴的交点为E,先求出直线AC的解析式,再取出点E的坐标,然后求出△ACB的面积,再根据三角形的面积求出DE的长度,然后分点D在点E的上方与下方两种情况写出点D的坐标即可.
点评:本题考查了待定系数法求二次函数解析式,二次函数的性质,难点在于要分点D在AC的上方与下方两种情况讨论.

练习册系列答案
相关题目
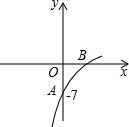 已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.
已知抛物线y=(1-a)x2+8x+b的图象的一部分如图所示,抛物的顶点在第一象限,且经过点A(0,-7)和点B.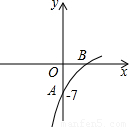
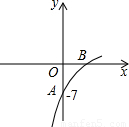
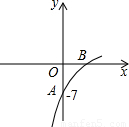
 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.