Question

【题目】将一个直角三角形纸片放置在平面直角坐标系中，点．

(1)点为边上一点(点不与重合)，沿将纸片折叠得的对应点，边与轴交于点．

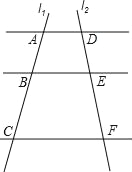
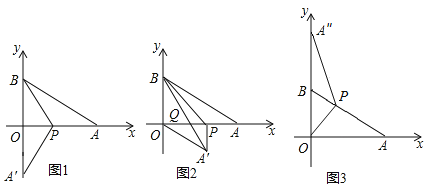
①如图1，当点刚好落在轴上时，求点的坐标

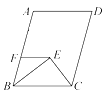
②如图2，当时，若线段在轴上移动得到线段(线段平移时不动)，当△A′O′Q′周长最小时，求OO′的长度．

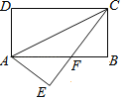
(2)如图3，若点为边上一点(点不与重合)，沿将纸片折叠得的对应点，当时，求点的坐标．

Answer 1

【答案】（1）①A'（0，-1）；②；（2）

【解析】

（1）①先利用勾股定理求出AB=2，根据折叠求出BA'，再利用线段的和差求出OA'即可得出结论；
②先由折叠求出∠BPA=135°，进而求出OP=1，即可求出PA'，求出点A'的坐标，从而求出直线A'B的解析式，求出OQ的长度，最后用等腰三角形的三线合一即可得出结论；
（2）先求出∠OPA=105°，再构造直角三角形，建立方程即可求出结论．

解：（1）①∵A（，0），B（0，1），
∴OA=，OB=1，根据勾股定理得，AB=2，

由折叠知，BA'=BA=2，PA=PA'，
∴OA'=BA'-OB=1，
∴A'（0，-1）；
②∵A′P⊥OA，
∴∠APA'=90°，
由折叠知，∠BPA=∠BPA'=（360°-∠APA'）=135°，
∴∠BPO=45°，
∴OP=OB=1，

∴PA'=PA=OA-OP=-1，
∴A'（1，1-），
∵B（0，1），
∴直线A'B的解析式为y=-x+1，
令y=0，得，-x+1=0，

，∴Q（，0），
∴OQ=，
∵线段OQ在x轴上移动得到线段O′Q′（线段OQ平移时A′不动），要△A′O′Q′周长最小，
则有，PA'是O'Q的垂直平分线，P是垂足，

（2）如图，

在Rt△AOB中，

∴∠OAB=30°
∵∠BPA'=30°，
∴∠APA'=150°，
由折叠知，∠APO=∠A'PO=（360°-150°）=105°，
过点P作PG⊥OA于G，
在Rt△PGA中，∠APG=60°，
∴∠OPG=45°，
设PG=m，
在Rt△POG中，AG=PG=m，
在Rt△PGO中，OG=PG=m，
∴OA=OG+AG=m+m=，