ĢāÄæÄŚČŻ
£Ø2012•¹°ŹūĒų¶žÄ££©ČēĶ¼£¬ŅŃÖŖĢŻŠĪABCDµÄĻĀµ×±ß³¤AB=8cm£¬ÉĻµ×±ß³¤DC=1cm£¬OĪŖABµÄÖŠµć£¬ĢŻŠĪµÄøßDO=4cm£®¶ÆµćP×ŌAµć³ö·¢£¬ŌŚABÉĻŌČĖŁŌĖŠŠ£¬¶ÆµćQ×ŌµćB³ö·¢£¬ŃŲB”śC”śD”śAŌČĖŁŌĖŠŠ£¬ĖŁ¶Č¾łĪŖĆæĆė1øöµ„Ī»£¬µ±ĘäÖŠŅ»øö¶Æµćµ½“ļÖÕµćŹ±£¬Įķ Ņ»¶ÆµćŅ²Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćPŌĖ¶Æt£ØĆė£©Ź±£¬”÷OPQµÄĆ껿ĪŖS£Ø²»Äܹ¹³É”÷OPQµÄ¶Æµć³żĶā£©£®
Ņ»¶ÆµćŅ²Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćPŌĖ¶Æt£ØĆė£©Ź±£¬”÷OPQµÄĆ껿ĪŖS£Ø²»Äܹ¹³É”÷OPQµÄ¶Æµć³żĶā£©£®
£Ø1£©ĒóSĖęt±ä»ÆµÄŗÆŹż¹ŲĻµŹ½¼°tµÄȔֵ·¶Ī§£»
£Ø2£©µ±tĪŖŗĪÖµŹ±SµÄÖµ×ī“ó£æĖµĆ÷ĄķÓÉ£®
 Ņ»¶ÆµćŅ²Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćPŌĖ¶Æt£ØĆė£©Ź±£¬”÷OPQµÄĆ껿ĪŖS£Ø²»Äܹ¹³É”÷OPQµÄ¶Æµć³żĶā£©£®
Ņ»¶ÆµćŅ²Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčµćPŌĖ¶Æt£ØĆė£©Ź±£¬”÷OPQµÄĆ껿ĪŖS£Ø²»Äܹ¹³É”÷OPQµÄ¶Æµć³żĶā£©£®£Ø1£©ĒóSĖęt±ä»ÆµÄŗÆŹż¹ŲĻµŹ½¼°tµÄȔֵ·¶Ī§£»
£Ø2£©µ±tĪŖŗĪÖµŹ±SµÄÖµ×ī“ó£æĖµĆ÷ĄķÓÉ£®
·ÖĪö£ŗ£Ø1£©ĻČ·Ö±šĒó³öµ±0£¼t£¼4Ź±£¬µ±4£¼t”Ü5Ź±£¬µ±5£¼t”Ü6Ź±£¬µ±6£¼t”Ü8Ź±£¬”÷OPQµÄµ×±ßŗĶøߣ¬ŌŁøł¾ŻĆ껿¹«Ź½¼“æÉĒó³öSĖęt±ä»ÆµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©·Ö±šĒó³öµ±0£¼t£¼4Ź±£¬µ±4£¼t”Ü5Ź±£¬µ±5£¼t”Ü6Ź±£¬µ±6£¼t”Ü8Ź±£¬S”÷OPQµÄ×ī“óÖµ£¬Č»ŗóÕŅ³öĖÄøö½į¹ūÖŠ×ī“óµÄ¼“æÉ£®
£Ø2£©·Ö±šĒó³öµ±0£¼t£¼4Ź±£¬µ±4£¼t”Ü5Ź±£¬µ±5£¼t”Ü6Ź±£¬µ±6£¼t”Ü8Ź±£¬S”÷OPQµÄ×ī“óÖµ£¬Č»ŗóÕŅ³öĖÄøö½į¹ūÖŠ×ī“óµÄ¼“æÉ£®
½ā“š£ŗ½ā£ŗ£Ø1£©¹żµćC×÷CE”ĶAB£¬“¹×ćĪŖE£¬
”ßCD=1£¬
”ąOE=1£¬
”ßOĪŖABµÄÖŠµć£¬AB=8£¬
”ąOB=OA=4£¬
”ąEB=4-1=3£¬
”ßOD=4£¬
”ąCE=4£¬
”ąBC=5£¬
¢ŁČēĶ¼£Ø1£©£¬µ±0£¼t£¼4Ź±£¬µćQŌŚBCÉĻ£¬µćPŌŚµćO×ó²ąŹ±£¬
¹żµćQ×÷QF”ĶAB£¬
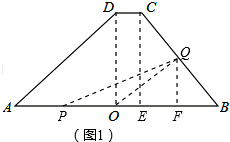
ŌņPO=4-t£¬BQ=t£¬
=
£¬
=
£¬
QF=
t£¬
S”÷OPQ=
PO•QF=
£Ø4-t£©•
t=
t-
t2£»
¢ŚČēĶ¼£Ø2£©£¬µ±4£¼t”Ü5Ź±£¬
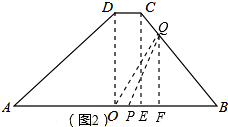
OP=t-4£¬QF=
t£¬
S”÷OPQ=
PO•QF=
£Øt-4£©•
t=
t2-
t£»
¢ŪČēĶ¼£Ø3£©£¬µ±5£¼t”Ü6Ź±£¬
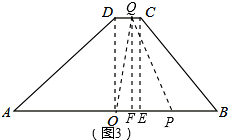
OP=t-4£¬QF=4£¬
S”÷OPQ=
PO•QF=
£Øt-4£©”Į4=2t-8£»
¢ÜČēĶ¼£Ø4£©£¬µ±6£¼t”Ü8Ź±£¬
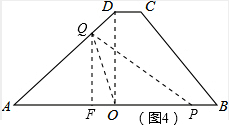
ӧOA=OD=4
”ąAD=
=4
£¬
”ąAD+CD+CB=4
+1+5=6+4
£¬
”ąAQ=6+4
-t£¬
ӧ
=
£¬
”ą
=
£¬
”ąQF=
=4-
£Øt-6£©£¬
”ąS”÷OPQ=
PO•QF=
£Øt-4£©”Į[4-
£Øt-6£©]=-
t2+
t-8-6
£»
£Ø2£©µ±0£¼t£¼4Ź±£¬t=2S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ
£»
µ±4£¼t”Ü5Ź±£¬t=5S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ2£»
µ±5£¼t”Ü6Ź±£¬t=6S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ4£»
µ±6£¼t”Ü8Ź±£¬t=5+2
S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ2+
£¬
Ōņt=5+2
S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ2+
£®
”ßCD=1£¬
”ąOE=1£¬
”ßOĪŖABµÄÖŠµć£¬AB=8£¬
”ąOB=OA=4£¬
”ąEB=4-1=3£¬
”ßOD=4£¬
”ąCE=4£¬
”ąBC=5£¬
¢ŁČēĶ¼£Ø1£©£¬µ±0£¼t£¼4Ź±£¬µćQŌŚBCÉĻ£¬µćPŌŚµćO×ó²ąŹ±£¬
¹żµćQ×÷QF”ĶAB£¬

ŌņPO=4-t£¬BQ=t£¬
| QF |
| CE |
| BQ |
| BC |
| QF |
| 4 |
| t |
| 5 |
QF=
| 4 |
| 5 |
S”÷OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 8 |
| 5 |
| 2 |
| 5 |
¢ŚČēĶ¼£Ø2£©£¬µ±4£¼t”Ü5Ź±£¬

OP=t-4£¬QF=
| 4 |
| 5 |
S”÷OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 8 |
| 5 |
¢ŪČēĶ¼£Ø3£©£¬µ±5£¼t”Ü6Ź±£¬

OP=t-4£¬QF=4£¬
S”÷OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
¢ÜČēĶ¼£Ø4£©£¬µ±6£¼t”Ü8Ź±£¬

ӧOA=OD=4
”ąAD=
| 42+42 |
| 2 |
”ąAD+CD+CB=4
| 2 |
| 2 |
”ąAQ=6+4
| 2 |
ӧ
| AQ |
| AD |
| QF |
| OD |
”ą
6+4
| ||
4
|
| QF |
| 4 |
”ąQF=
24+16
| ||
4
|
| ||
| 2 |
”ąS”÷OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
5
| ||
| 2 |
| 2 |
£Ø2£©µ±0£¼t£¼4Ź±£¬t=2S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ
| 8 |
| 5 |
µ±4£¼t”Ü5Ź±£¬t=5S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ2£»
µ±5£¼t”Ü6Ź±£¬t=6S”÷OPQ×ī“ó£¬S”÷OPQµÄ×ī“óÖµĪŖ4£»
µ±6£¼t”Ü8Ź±£¬t=5+2
| 2 |
9
| ||
| 4 |
Ōņt=5+2
| 2 |
9
| ||
| 4 |
µćĘĄ£ŗ“ĖĢāæ¼²éĮĖĻąĖĘŠĪµÄ×ŪŗĻ£¬ÓƵ½µÄÖŖŹ¶µćŹĒĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ”¢¶ž“ĪŗÆŹżµÄ×īÖµ”¢¹“¹É¶ØĄķµČ£¬¹Ų¼üŹĒøł¾ŻĢāŅā»³ö·ūŗĻŅŖĒóµÄĖłÓŠĶ¼ŠĪ£®

Į·Ļ°²įĻµĮŠ“š°ø
 ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø
ĶسĒѧµäĬŠ“ÄÜŹÖĻµĮŠ“š°ø
Ļą¹ŲĢāÄæ
 £Ø2012•¹°ŹūĒų¶žÄ££©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬?ABCOµÄ¶„µćAŌŚxÖįÉĻ£¬¶„µćBµÄ×ų±źĪŖ£Ø4£¬6£©£®ČōÖ±Ļßy=kx+3k½«?ABCO·Öøī³ÉĆ껿ĻąµČµÄĮ½²æ·Ö£¬ŌņkµÄÖµŹĒ£Ø””””£©
£Ø2012•¹°ŹūĒų¶žÄ££©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬?ABCOµÄ¶„µćAŌŚxÖįÉĻ£¬¶„µćBµÄ×ų±źĪŖ£Ø4£¬6£©£®ČōÖ±Ļßy=kx+3k½«?ABCO·Öøī³ÉĆ껿ĻąµČµÄĮ½²æ·Ö£¬ŌņkµÄÖµŹĒ£Ø””””£©