Question

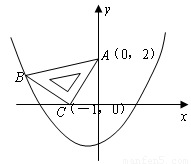
如图所示的平面直角坐标系，完成以下各题。

（1）写出图中点A、B、C、D的坐标；   
（2）在此平面直角坐标中描出点E（1，0），F（0，-2），G（-1，0），H（0，2）；  
（3）顺次连接A、B、C、D各点，再连接EF、FG、GH、HE，分别计算围成的两个封闭图形的面积。

Answer 1

解：（1）图中所求各点的坐标分别为A（2，2），B（-2，2），C（-2，-2），D（2，-2）。
（2）如答图所示：
；
（3）顺次连接A、B、C、D各点，得到一个正方形，它的面积为4×4=16 ，顺次连接E、F、G、H 各点，得到四边形EFGH 的面积为△EGH 和△EGF 的面积和，即为×2×2+×22=4，故正方形ABCD的面积为16，四边形EFGH的面积为4。