题目内容
阅读下面的内容
用换元法求解方程组的解
题目:已知方程组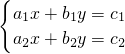 ①的解是
①的解是 ,
,
求方程组 ②的解.
②的解.
解:方程组 ②可以变形为:方程组
②可以变形为:方程组 ③
③
设2x=m,3y=n,则方程组③可化为 ④
④
比较方程组④与方程组①可得 ,即
,即
所以方程组②的解为
参考上述方法,解决下列问题:
(1)若方程组 的解是
的解是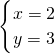 ,则方程组
,则方程组 的解为______;
的解为______;
(2)若方程组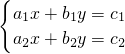 ①的解是
①的解是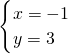 ,求方程组
,求方程组 ②的解.
②的解.
解:(1)根据题意得:x+1=2,y-2=3,
解得:x=1,y=5,
则方程组的解为: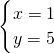 ;
;
(2)根据题意得:x-2=-1,2y=3,即x=1,y= ,
,
则方程组的解为: .
.
分析:(1)根据题意列出x与y的方程,分别求出方程的解即可得到方程组的解;
(2)根据题意列出x与y的方程,分别求出方程的解即可得到方程组的解.
点评:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.弄清题意是解本题的关键.
解得:x=1,y=5,
则方程组的解为:
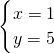 ;
;(2)根据题意得:x-2=-1,2y=3,即x=1,y=
 ,
,则方程组的解为:
 .
.分析:(1)根据题意列出x与y的方程,分别求出方程的解即可得到方程组的解;
(2)根据题意列出x与y的方程,分别求出方程的解即可得到方程组的解.
点评:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.弄清题意是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目