题目内容
如图，在平面直角坐标系xoy中，一次函数
的图象与x轴交于A（－1，0），与y轴交于点C.以直线x=2为对称轴的抛物线
经过A、C两点，并与x轴正半轴交于点B.
（1）（3分）求m的值及抛物线
的函数表达式.
（2）（5分）设点
，若F是抛物线对称轴上使得△ADF的周长取得最小值的点，过F任意作一条与y轴不平行的直线交抛物线
于
两点，试探究
是否为定值？请说明理由.
（3）（4分）将抛物线C1作适当平移，得到抛物线
，若当
时，
恒成立，求m的最大值.
（1）
,抛物线
…………………………………… 3′
（2）要使△ADF周长最小，只需AD+FD最小，
∵A与B关于x=2对称
∴只
需BF+DF最小
又∵BF+DF≥BD
∴F为BD与x=2的交点
BD直线为
，当x=2时
∴
∵
∴
同理
∴
又∵
∴
∴
∴
……………………………… 8′
（3）法一：
设
的两根分别为
∵抛物线
可以看成由
左右平移得到，观察图象可知，随着图象向右移，的值不断增大
∴当
学习恒成立时，
最大值在
处取得
∴当
时，对应的即为的最大值
将代入
得
∴
10′
将
代入有
∴
∴的最大值为9 ………………………………… 12′
法二：
恒成立
化简得
，
，恒成立
设
，如图则有
10′
即
∴
∴的最大值为9 …………………………
名校练考卷期末冲刺卷系列答案下列叙述正确的是（ ）
|
| A． | 方差越大，说明数据就越稳定 |
|
| B． | 在不等式两边同乘或同除以一个不为0的数时，不等号的方向不变 |
|
| C． | 不在同一直线上的三点确定一个圆 |
|
| D． | 两边及其一边的对角对应相等的两个三角形全等 |
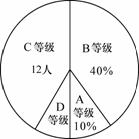
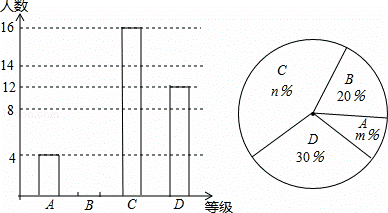
学校举行“文明环保，从我做起”征文比赛.现有甲、乙两班各上交30篇作文，现将两班的各30篇作文的成绩（单位：分）统计如下：
甲班： 
乙班：
| 等级 | 成绩（S ） | 频数 |
| A | 90＜S≤100 | x |
| B | 80＜S≤90 | 15 |
| C | 70＜S≤80 | 10 |
| D | S≤70 | 3 |
| 合计 | 30 |
第19题图
根据上面提供的信息回答下列问题
⑴（3分）表中x= ，甲班学生成绩的中位数落在等级 中，扇形统计图中等级D部分的扇形圆心角n= .
⑵（5分）现学校决定从两班所有A等级成绩的学生中随机抽取2名同学参加市级征文比赛.求抽取到两名学生恰好来自同一班级的概率（请列树状图或列表求解）.
；