题目内容
 如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,求∠OBC的余弦值.
如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,求∠OBC的余弦值.分析:首先连接CD,由90°的圆周角所对的弦是直径,可得CD是直径,则可求得sin∠ODC=
,即可得∠ODC的度数,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,求得∠OBC的度数,根据特殊角的三角函数值,即可求得答案.
| 1 |
| 2 |
解答: 解:连接CD,
解:连接CD,
∵∠COD=90°,
∴CD为直径,
∵直径为10,
∴CD=10,
∵点C(0,5)和点O(0,0),
∴OC=5,
∴sin∠ODC=
=
,
∴∠ODC=30°,
∴∠OBC=∠ODC=30°,
∴cos∠OBC=cos30°=
.
 解:连接CD,
解:连接CD,∵∠COD=90°,
∴CD为直径,
∵直径为10,
∴CD=10,
∵点C(0,5)和点O(0,0),
∴OC=5,
∴sin∠ODC=
| OC |
| CD |
| 1 |
| 2 |
∴∠ODC=30°,
∴∠OBC=∠ODC=30°,
∴cos∠OBC=cos30°=
| ||
| 2 |
点评:此题考查了圆周角定理、特殊角的三角函数值的知识.此题难度适中,解题的关键是准确作出辅助线,掌握90°的圆周角所对的弦是直径与在同圆或等圆中,同弧或等弧所对的圆周角相等定理的应用,熟记特殊角的三角函数值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•和平区二模)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的正弦值为( )
(2013•和平区二模)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的正弦值为( )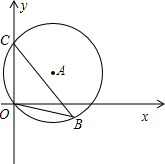 (2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
(2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( ) (2012•瑶海区三模)如图,直径为10的⊙A经过点C和点O,点B是y轴右侧⊙A优弧上一点,∠OBC=30°,则点C的坐标为( )
(2012•瑶海区三模)如图,直径为10的⊙A经过点C和点O,点B是y轴右侧⊙A优弧上一点,∠OBC=30°,则点C的坐标为( )