��Ŀ����
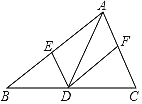
����Ŀ����ͼ����������x�ύ�ڵ�A����5��0���͵�B��3��0������y�ύ�ڵ�C��0��5������һ����Ϊ1�������㹻�ľ��Σ���Ӱ���֣���x�᷽��ƽ�ƣ���y��ƽ�е�һ��Ա߽��������ڵ�P��Q����ֱ��AC�ڵ�M��N����x���ڵ�E��F��
��1���������ߵĽ���ʽ��
��2������M��N�����߶�AC��ʱ������MF�����sin��AMF= ![]() �����Q�����ꣻ
�����Q�����ꣻ
��3���ھ��ε�ƽ�ƹ����У����Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ�����M�����꣮
���𰸡�
��1��
�⣺����������x�ύ�ڵ�A����5��0����B��3��0����
����Լ���������Ϊy=a��x+5����x��3�����ѵ㣨0��5������õ�a=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2��
x2�� ![]() x+5��
x+5��
��2��
�⣺����FG��AC��G�����F���꣨m��0����
��AF=m+5��AE=EM=m+6��FG= ![]() ��m+5����FM=
��m+5����FM= ![]() =
= ![]() ��
��
��sin��AMF= ![]() ��
��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() �������õ�2m2+19m+44=0��
�������õ�2m2+19m+44=0��
�ࣨm+4����2m+11��=0��
��m=��4��5.5����������
���Q���꣨��4�� ![]() ��
��
��3��
�⣺

�ٵ�MN�ǶԽ���ʱ�����F��m��0����
��ֱ��AC����ʽΪy=x+5��
���N��m��m+5������M��m+1��m+6����
��QN=PM��
�ੁ ![]() m2��
m2�� ![]() m+5��m��5=m+6��[��
m+5��m��5=m+6��[�� ![]() ��m+1��2��
��m+1��2�� ![]() ��m+1��+5]��
��m+1��+5]��
���m=��3�� ![]() ��
��
���M���꣨��2+ ![]() ��3+
��3+ ![]() ����2��
����2�� ![]() ��3��
��3�� ![]() ����
����
�ڵ�MNΪ��ʱ��MN=PQ= ![]() �����Q��m����
�����Q��m���� ![]() m2��
m2�� ![]() m+5�����P��m+1����
m+5�����P��m+1���� ![]() m2��
m2�� ![]() m+6����
m+6����
�ੁ ![]() m2��
m2�� ![]() m+6=��
m+6=�� ![]() ��m+1��2��
��m+1��2�� ![]() ��m+1��+5��
��m+1��+5��
���m=��3��
���M���꣨��2��3����
���������Ե�P��Q��M��NΪ������ı�����ƽ���ı���ʱ����M������Ϊ����2��3����2+ ![]() ��3+
��3+ ![]() ����2��
����2�� ![]() ��3��
��3�� ![]() ����
����
����������1����������Ϊy=a��x+5����x��3�����ѵ㣨0��5�����뼴�ɽ�����⣮��2����FG��AC��G�����F���꣨m��0��������sin��AMF= ![]() =
= ![]() ���г����̼��ɽ�����⣮��3���ٵ�MN�ǶԽ���ʱ�����F��m��0������QN=PM���г����̼��ɽ�����⣮�ڵ�MNΪ��ʱ��MN=PQ=
���г����̼��ɽ�����⣮��3���ٵ�MN�ǶԽ���ʱ�����F��m��0������QN=PM���г����̼��ɽ�����⣮�ڵ�MNΪ��ʱ��MN=PQ= ![]() �����Q��m����
�����Q��m���� ![]() m2��
m2�� ![]() m+5�����P��m+1����
m+5�����P��m+1���� ![]() m2��
m2�� ![]() m+6�������������߽���ʽ���ⷽ�̼��ɣ����⿼����κ����ۺ��⡢���Ǻ��������ɶ�����֪ʶ������Ĺؼ���ѧ�����ϵ����ȷ����������ʽ��ѧ��������ۣ��÷��̵�˼�������⣬�����п�ѹ���⣮
m+6�������������߽���ʽ���ⷽ�̼��ɣ����⿼����κ����ۺ��⡢���Ǻ��������ɶ�����֪ʶ������Ĺؼ���ѧ�����ϵ����ȷ����������ʽ��ѧ��������ۣ��÷��̵�˼�������⣬�����п�ѹ���⣮
�����㾫�������ڱ��⿼��Ķ��κ�����ͼ��Ͷ��κ��������ʣ���Ҫ�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�

 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�����Ŀ���Ӽص��ҵ���![]() ������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
��������ʱ��Ƶ�� ��������ʱ��· |
|
|
|
| �ϼ� |
| 59 | 151 | 166 | 124 | 500 |
| 50 | 50 | 122 | 278 | 500 |
| 45 | 265 | 160 | 30 | 500 |
��߷��ڼ䣬����_________������![]() ������
������![]() ������
������![]() ������·�ϵĹ��������Ӽص��ҵ�����ʱ������45�������Ŀ��������
������·�ϵĹ��������Ӽص��ҵ�����ʱ������45�������Ŀ��������