题目内容
【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA= ![]() ,cot∠ABC=
,cot∠ABC= ![]() ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长.
【答案】
(1)
【答案】解:∵CD⊥AB,AD=8,tanA= ![]() ,
,
在Rt△ACD中,tanA= ![]() =
= ![]() ,AD=8,CD=4,
,AD=8,CD=4,
在Rt△CBD,cot∠ABC= ![]() =
= ![]() ,BD=3,
,BD=3,
∴⊙D的半径为3
(2)
解:过圆心D作DH⊥BC,垂足为H,
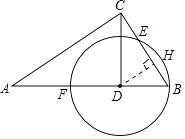
∴BH=EH,
在Rt△CBD中∠CDB=90°,BC= ![]() =5,cos∠ABC=
=5,cos∠ABC= ![]() =
= ![]() ,
,
在Rt△BDH中,∠BHD=90°,cos∠ABC= ![]() =
= ![]() ,BD=3,BH=
,BD=3,BH= ![]() ,
,
∵BH=EH,
∴BE=2BH= ![]() ,
,
∴CE=BC﹣BE=5﹣ ![]() =
= ![]() .
.
【解析】(1)根据三角函数的定义得出CD和BD,从而得出⊙D的半径;
(2)过圆心D作DH⊥BC,根据垂径定理得出BH=EH,由勾股定理得出BC,再由三角函数的定义得出BE,从而得出CE即可.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

【题目】某校在“626国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
少分数段(x表示分数) | 频数 | 频率 |
50≤x<60 | 4 | 0.1 |
60≤x<70 | a | 0.2 |
70≤x<80 | 12 | b |
80≤x<90 | 10 | 0.25 |
90≤x<100 | 6 | 0.15 |

(1)表中a= , b= , 并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是;
(3)请估计该年级分数在60≤x<100的学生有多少人?