题目内容
如图，点C是线段AB的中点，DA⊥AB，EB⊥AB，DC=EC，求证：△ACD≌△BCE．
证明：∵DA⊥AB，EB⊥AB，
∴∠A=∠B=90°，
∵点C是线段AB的中点，
∴AC=BC，
在Rt△ADC和Rt△BEC中
，
∴Rt△ADC≌Rt△BEC（HL）．
分析：首先说明△ADC和△BEC是直角三角形，再利用HL定理证明Rt△ADC≌Rt△BEC即可．
点评：此题主要考查了全等三角形的判定，关键是掌握HL定理．
∴∠A=∠B=90°，
∵点C是线段AB的中点，
∴AC=BC，
在Rt△ADC和Rt△BEC中
，∴Rt△ADC≌Rt△BEC（HL）．
分析：首先说明△ADC和△BEC是直角三角形，再利用HL定理证明Rt△ADC≌Rt△BEC即可．
点评：此题主要考查了全等三角形的判定，关键是掌握HL定理．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
如图，点C是线段AB的中点，点D是线段BC的中点，下面等式不正确的是（ ）
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
10、如图，点D是线段AB与线段BC的垂直平分线的交点，∠B=40°，则∠ADC等于（ ）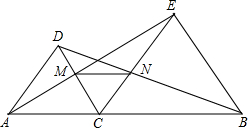
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD和CE相交于点N．
如图，点C是线段AB的中点，点D是线段CB上任意一点，则下列表示线段关系的式子不正确的是（ ）
如图，点C是线段AB的中点，点D是线段BC的中点，则下列结论中错误的是（ ）