题目内容
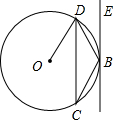 如图,已知BE是⊙O的切线,点C、D在⊙O上,∠DCB=40°,则∠EBD=
如图,已知BE是⊙O的切线,点C、D在⊙O上,∠DCB=40°,则∠EBD=40
40
度.分析:连接OB,由EB为圆O的切线,得到OB垂直于EB,可得出∠OBE为直角,再由同弧所对的圆心角等于所对圆周角的2倍,由∠BCD的度数求出∠BOD的度数,再由OD=OB,利用三角形的内角和定理,根据顶角求出底角∠OBD的度数,根据∠EBD=∠OBE-∠OBD即可求出∠EBD的度数.
解答:解:连接OB,如图所示:
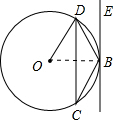
∵圆心角∠BOD与圆周角∠BCD都对
,且∠DCB=40°,
∴∠BOD=80°,
又∵OD=OB,
∴∠OBD=∠ODB=
=50°,
又∵EB为圆O的切线,
∴OB⊥BE,
∴∠OBE=90°,
又∵∠OBD=50°,
则∠EBD=∠OBE-∠OBD=90°-50°=40°.
故答案为:40.

∵圆心角∠BOD与圆周角∠BCD都对
 |
| DB |
∴∠BOD=80°,
又∵OD=OB,
∴∠OBD=∠ODB=
| 180°-80° |
| 2 |
又∵EB为圆O的切线,
∴OB⊥BE,
∴∠OBE=90°,
又∵∠OBD=50°,
则∠EBD=∠OBE-∠OBD=90°-50°=40°.
故答案为:40.
点评:此题考查了切线的性质,圆周角定理,以及等腰三角形的性质,利用了转化的思想,遇到直线与圆相切,常常连接圆心与切点,利用切线的性质得出垂直,根据直角三角形的性质来解决问题.

练习册系列答案
相关题目
 12、(1)世界上最大的动物是鲸,有一种鲸体重达7.5×104千克,世界上最小的一种鸟--蜂鸟,体重仅2克,则这种鲸是蜂鸟的体重的
12、(1)世界上最大的动物是鲸,有一种鲸体重达7.5×104千克,世界上最小的一种鸟--蜂鸟,体重仅2克,则这种鲸是蜂鸟的体重的 如图,已知BE是△ABC的高,AE=BE,
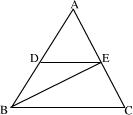
如图,已知BE是△ABC的高,AE=BE, 如图,已知BE是∠ABC的平分线,DE∥BC,∠ADE=50°,则∠EBC=
如图,已知BE是∠ABC的平分线,DE∥BC,∠ADE=50°,则∠EBC= (1)世界上最大的动物是鲸,有一种鲸体重达7.5×104千克,世界上最小的一种鸟--蜂鸟,体重仅2克,则这种鲸是蜂鸟的体重的______倍;
(1)世界上最大的动物是鲸,有一种鲸体重达7.5×104千克,世界上最小的一种鸟--蜂鸟,体重仅2克,则这种鲸是蜂鸟的体重的______倍;