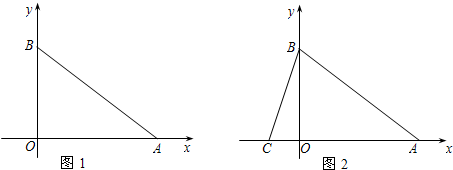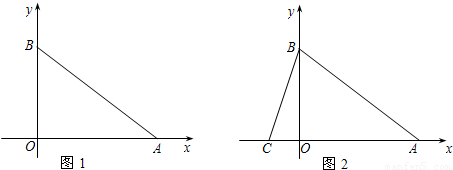题目内容
已知:一个等腰直角三角形腰长为a,三边上的高之积为P,一个等边三角形边长为a,三边上的高之积为Q,则P和Q的大小关系是
- A.P>Q
- B.P<Q
- C.P=Q
- D.无法确定
A
分析:分别求得等腰直角三角形和等边三角形三边上的高的积,然后利用做差法比较两者的大小,从而求得结果.
解答:如左图,在△ABC中,AB=AC=a,∠A=90°,
过A作AD⊥BC于点D,
∵AB=AC=a,∠A=90°,
∴BD=DC= a,
a,
∴P=a×a× a=
a= a3,
a3,
如右图,在△ABC中,AB=AC=BC=a
过A作AD⊥BC于点D,
∵∠B=60°BD=DC= a,
a,
∴AD= a,
a,
同理,其它边上的高也与AD相等.
∴Q=( a)3=
a)3= a3,
a3,
∵P-Q= a3-
a3- a3>0,
a3>0,
∴P>Q.
故选A.
点评:主要考查等腰直角三角形和等边三角形的性质,考查解直角三角形的定义,由直角三角形已知元素求未知元素的过程.
分析:分别求得等腰直角三角形和等边三角形三边上的高的积,然后利用做差法比较两者的大小,从而求得结果.
解答:如左图,在△ABC中,AB=AC=a,∠A=90°,
过A作AD⊥BC于点D,
∵AB=AC=a,∠A=90°,

∴BD=DC=
 a,
a,∴P=a×a×
 a=
a= a3,
a3,如右图,在△ABC中,AB=AC=BC=a
过A作AD⊥BC于点D,
∵∠B=60°BD=DC=
 a,
a,∴AD=
 a,
a,同理,其它边上的高也与AD相等.

∴Q=(
 a)3=
a)3= a3,
a3,∵P-Q=
 a3-
a3- a3>0,
a3>0,∴P>Q.
故选A.
点评:主要考查等腰直角三角形和等边三角形的性质,考查解直角三角形的定义,由直角三角形已知元素求未知元素的过程.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目