题目内容
 如图,一艘轮船由西向东航行,在A处测得北偏东68.7°反向有小岛C,继续前进60海里到达B处,此时测得小岛C在船的北偏东26.5°方向,则船继续向东航行
如图,一艘轮船由西向东航行,在A处测得北偏东68.7°反向有小岛C,继续前进60海里到达B处,此时测得小岛C在船的北偏东26.5°方向,则船继续向东航行考点:解直角三角形的应用-方向角问题
专题:
分析:过C作AB的垂线,交直线AB于点D,分别在Rt△ACD与Rt△BCD中用式子表示CD,从而求得BD的值,即离小岛C最近的距离.
解答: 解:过C作AB的垂线,交直线AB于点D,
解:过C作AB的垂线,交直线AB于点D,
得到Rt△ACD与Rt△BCD.
设CD=x海里,在Rt△BCD中,tan∠CBD=
,
∴BD=
,
在Rt△ACD中,tanA=
,
∴AD=
,
∴AD-BD=AB,即
-
=60,
解得,x=30.
BD=
≈15(海里).
答:轮船继续向东航行15海里,距离小岛C最近.
 解:过C作AB的垂线,交直线AB于点D,
解:过C作AB的垂线,交直线AB于点D,得到Rt△ACD与Rt△BCD.
设CD=x海里,在Rt△BCD中,tan∠CBD=
| CD |
| BD |
∴BD=
| x |
| tan63.5° |
在Rt△ACD中,tanA=
| CD |
| AD |
∴AD=
| x |
| tan21.3° |
∴AD-BD=AB,即
| x |
| tan21.3° |
| x |
| tan63.5° |
解得,x=30.
BD=
| 30 |
| tan63.5° |
答:轮船继续向东航行15海里,距离小岛C最近.
点评:本题考查了解直角三角形的应用-方向角问题,解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
 △ABC中,D为BC边的中点,延长AD至E、延长AB交CE于P,若AD=2DE,求证:AP=3AB.
△ABC中,D为BC边的中点,延长AD至E、延长AB交CE于P,若AD=2DE,求证:AP=3AB.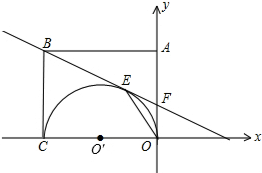 如图,矩形OABC的两边OC、OA分别是x轴和y轴上,过点B的直线切以OC为直径的半圆O′于点E,交y轴于点F,连接OE,且已知C(-6,0),F(0,2).试求点B的坐标.
如图,矩形OABC的两边OC、OA分别是x轴和y轴上,过点B的直线切以OC为直径的半圆O′于点E,交y轴于点F,连接OE,且已知C(-6,0),F(0,2).试求点B的坐标.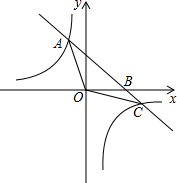 如图,已知直线y=-x+4与反比例函数y=
如图,已知直线y=-x+4与反比例函数y=