题目内容
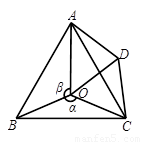
如图,点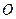 是等边
是等边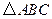 内一点,
内一点,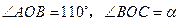 .将
.将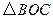 绕点
绕点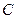 按顺时针方向旋转
按顺时针方向旋转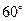 得
得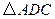 ,连接
,连接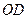
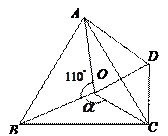
【小题1】求证:
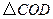 是等边三角形;
是等边三角形;【小题2】当
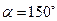 时,试判断
时,试判断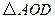 的形状,并说明理由
的形状,并说明理由【小题3】探究:当
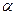 为多少度时,
为多少度时,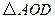 是等腰三角形?
是等腰三角形?
p;【答案】
【小题1】证明:∵OC=OD,∠OCD=60°,∴ △COD是等边三角形。…………(2分)
【小题2】当α=150°时,△AOD是Rt△。理由如下:………………………………(3分)
∵△COD为等边三角形,∴∠COD=∠CDO=60°
又∠ADC=α=150° ∴∠ADO=90°
【小题3】∵∠COD=∠CDO=60° ∠ADO=α-60°

∴∠AOD=360°-110°-60°-α=190°-α
∴∠OAD=180°-(190°-α)-(α-60°)=50°
① 若 190°-α=α-60° ∴ α=125°
② 若190°-α=50° ∴ α=140°
③ 若α-60°=50° ∴ α=110°
故 当α=125°或140°或110°时,△AOD是等腰三角形。解析:
p;【解析】略
【小题1】证明:∵OC=OD,∠OCD=60°,∴ △COD是等边三角形。…………(2分)
【小题2】当α=150°时,△AOD是Rt△。理由如下:………………………………(3分)
∵△COD为等边三角形,∴∠COD=∠CDO=60°
又∠ADC=α=150° ∴∠ADO=90°
【小题3】∵∠COD=∠CDO=60° ∠ADO=α-60°

∴∠AOD=360°-110°-60°-α=190°-α
∴∠OAD=180°-(190°-α)-(α-60°)=50°
① 若 190°-α=α-60° ∴ α=125°
② 若190°-α=50° ∴ α=140°
③ 若α-60°=50° ∴ α=110°
故 当α=125°或140°或110°时,△AOD是等腰三角形。解析:
p;【解析】略

练习册系列答案
相关题目
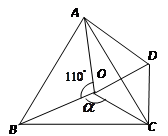

 是等边
是等边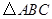 内一点,
内一点,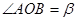 ,
, 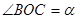 .将
.将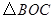 绕点
绕点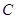 按顺时针方向旋转
按顺时针方向旋转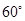 得
得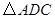 ,连接
,连接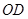 .
.
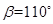 ,
,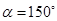 时,试判断
时,试判断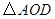 的形状,并说明理由.
的形状,并说明理由.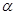 、
、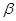 的度数.
的度数.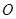 是等边
是等边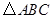 内一点,
内一点,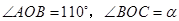 .将
.将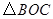 绕点
绕点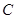 按顺时针方向旋转
按顺时针方向旋转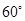 得
得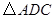 ,连接
,连接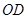

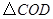 是等边三角形;
是等边三角形;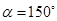 时,试判断
时,试判断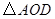 的形状,并说明理由
的形状,并说明理由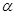 为多少度时,
为多少度时,