题目内容
如图,在□ABCD中,EF垂直平分AC交BC于E,交AD于F.

(1)求证:四边形AECF为菱形;
(2)若AC⊥CD,AB=6,BC=10,求四边形AECF的面积.
【答案】
(1)证明见解析; (2)24.
【解析】
试题分析:(1)先根据垂直平分线的性质得∴AE=EC,AF=FC,所以∠1=∠2,∠3=∠4;再结合平行线的性质得出∠1=∠4=∠3,即AF=AE,利用四条边相等的四边形是菱形即可证明;
(2)根据平行四边形的判定和性质, 勾股定理求出菱形AECF的两对角线长,即可根据菱形的面积公式求得.
试题解析:(1)∵EF垂直平分AC,∴AO=OC.∴∠1=∠2,∠3=∠4.
又∵四边形ABCD是平行四边形,∴AD∥BC. ∴∠1=∠4=∠3. ∴AF=AE.
∴AE=EC=CF=FA.∴四边形AECF是菱形.

(2)∵EF垂直平分AC,AC⊥CD,∴EF∥CD.
又∵四边形ABCD是平行四边形,∴AD∥BC. ∴四边形ECDF是平行四边形.
又∵AB=6,∴EF=CD= AB=6.
在Rt△ACD中, ∵CD=6,AD= BC=10,∴根据勾股定理,得AC=8.
∴四边形AECF的面积= ×AC×EF=24.
×AC×EF=24.
考点:1.平行四边形的性质;2.菱形的判定;3.等腰三角形的判定与性质;4. 勾股定理;5. 菱形的面积.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=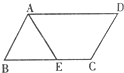 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.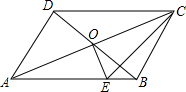 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是