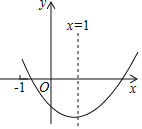ЬтФПФкШн
ЁОЬтФПЁПвбжЊЃКХзЮяЯпyЃНax2Љ3ЃЈaЉ1ЃЉx+2aЉ6ЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉЧѓжЄЃКХзЮяЯпгыxжсгаСНИіНЛЕуЃЎ
ЃЈ2ЃЉЩшХзЮяЯпгыxжсЕФСНИіНЛЕуЕФКсзјБъЗжБ№ЮЊx1ЃЌx2ЃЈЦфжаx1ЃОx2ЃЉЃЎШєtЪЧЙигкaЕФКЏЪ§ЁЂЧвtЃНax2Љx1ЃЌЧѓетИіКЏЪ§ЕФБэДяЪНЃЛ
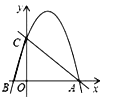
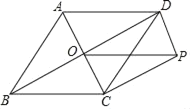
ЃЈ3ЃЉШєaЃН1ЃЌНЋХзЮяЯпЯђЩЯЦНвЦвЛИіЕЅЮЛКѓгыxжсНЛгкЕуAЁЂBЃЎЦНвЦКѓШчЭМЫљЪОЃЌЙ§AзїжБЯпACЃЌЗжБ№НЛyЕФе§АыжсгкЕуPКЭХзЮяЯпгкЕуCЃЌЧвOPЃН1ЃЎMЪЧЯпЖЮACЩЯвЛЖЏЕуЃЌЧѓ2MB+MCЕФзюаЁжЕЃЎ
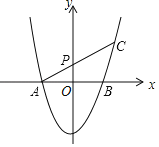
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉtЃНaЉ5ЃЛЃЈ3ЃЉ2MB+MCЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвЊжЄХзЮяЯпгыxжсгаСНИіНЛЕуЃЌПЩЧѓГіЖдгІЕФвЛдЊЖўДЮЗНГЬЕФИљЕФХаБ№ЪНЕФжЕЃЌРћгУЭъШЋЦНЗНЙЋЪНЕФЗЧИКадЫЕУїЁїЃО0МДПЩЃЛ
ЃЈ2ЃЉСюyЃН0ЃЌЧѓГіКЌaЕФСНИіНЛЕуЕФКсзјБъЃЌШЛКѓИљОнЬѕМўШЗЖЈx2КЭx1ЃЌдйДњШыtЃНax2Љx1жаећРэМДПЩЃЛ
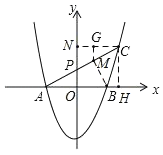
ЃЈ3ЃЉвзЧѓГіЦНвЦКѓХзЮяЯпЕФНтЮіЪНМАAЃЌBЕФзјБъКЭжБЯпACЕФНтЮіЪНЃЌШЛКѓСЊСЂжБЯпACЕФНтЮіЪНКЭЖўДЮКЏЪ§ЕФНтЮіЪНПЩЕУЕуCЕФзјБъЃЌЙ§CзїCNЁЭyжсЃЌЙ§MзїMGЁЭCNгкGЃЌЙ§CзїCHЁЭxжсгкHЃЌвзЕУЁЯGCMЃН30ЁуЃЌдђ![]() ЃЌгкЪЧ2MB+MCЃН2ЃЈMB+GMЃЉЃЌЖјMB+GMЕФзюаЁжЕМДBЕНCNЕФзюаЁОрРыCHЃЌЮЪЬтМДЕУНтОіЃЎ
ЃЌгкЪЧ2MB+MCЃН2ЃЈMB+GMЃЉЃЌЖјMB+GMЕФзюаЁжЕМДBЕНCNЕФзюаЁОрРыCHЃЌЮЪЬтМДЕУНтОіЃЎ
ЃЈ1ЃЉжЄУїЃКЁїЃНb2Љ4acЃН[Љ3ЃЈaЉ1ЃЉ]2Љ4aЃЈ2aЉ6ЃЉЃНa2+6a+9ЃНЃЈa+3ЃЉ2ЃЌ
ЁпaЃО0ЃЌЁрЃЈa+3ЃЉ2ЃО0ЃЌ
ЁрХзЮяЯпгыxжсгаСНИіНЛЕуЃЛ
ЃЈ2ЃЉНтЃКСюyЃН0ЃЌдђax2Љ3ЃЈaЉ1ЃЉx+2aЉ6ЃН0ЃЌ
ЁпaЃО0ЃЌЁр![]() ЃЌЁрx=2Лђ
ЃЌЁрx=2Лђ![]() ЃЌ
ЃЌ
ЁпaЃО0ЃЌЁр![]() ЃЌ
ЃЌ
Ёпx1ЃОx2ЃЌЁрx1ЃН2ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрtЃНaЉ5ЃЛ
ЃЈ3ЃЉНтЃКЕБaЃН1ЪБЃЌХзЮяЯпЮЊyЃНx2Љ4ЃЌЯђЩЯЦНвЦвЛИіЕЅЮЛЕУyЃНx2Љ3ЃЌ
СюyЃН0ЃЌдђx2Љ3ЃН0ЃЌНтЕУЃК![]() ЃЌЁрAЃЈ
ЃЌЁрAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ
ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЌЁрAOЃН
ЃЌ0ЃЉЃЌЁрAOЃН![]() ЃЌ
ЃЌ
ЁпOPЃН1ЃЌЁрPЃЈ0ЃЌ1ЃЉЃЌЩшжБЯпACЕФНтЮіЪНЮЊ![]() ЃЌАбЕуAЃЈ
ЃЌАбЕуAЃЈ![]() ЃЌ0ЃЉДњШыЃЌЕУЃК
ЃЌ0ЃЉДњШыЃЌЕУЃК![]() ЃЌЁржБЯпACЕФНтЮіЪНЮЊЃК
ЃЌЁржБЯпACЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
СЊСЂЃК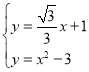 ЃЌНтЕУЃК
ЃЌНтЕУЃК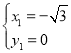 ЃЌ
ЃЌ ЃЌЁрЕуCзјБъЮЊЃЈ
ЃЌЁрЕуCзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дкRtЁїAOPжаЃЌИљОнЙДЙЩЖЈРэЃЌЕУЃКAPЃН![]() ЃЌЁрЁЯOAP=30ЁуЃЌ
ЃЌЁрЁЯOAP=30ЁуЃЌ
Й§CзїCNЁЭyжсЃЌЙ§MзїMGЁЭCNгкGЃЌЙ§CзїCHЁЭxжсгкHЃЌ
ЁпCNЁЮxжсЃЌЁрЁЯGCMЃНЁЯPAO=30ЁуЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпBЕНCNзюаЁОрРыЮЊCHЃЌ
ЁрMB+GMЕФзюаЁжЕЮЊCHЕФГЄЖШ![]() ЃЌ
ЃЌ
Ёр2MB+MCЕФзюаЁжЕЮЊ![]() ЃЎ
ЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ