题目内容
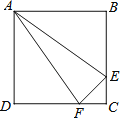
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. 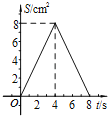 B.
B. 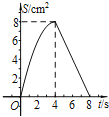
C. 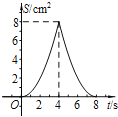 D.
D. 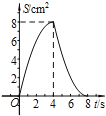
【答案】D
【解析】
试题分类讨论:当0≤t≤4时,利用S=S正方形ABCD﹣S△ADF﹣S△ABE﹣S△CEF可得S=﹣![]() t2+4t,配成顶点式得S=﹣
t2+4t,配成顶点式得S=﹣![]() (t﹣4)2+8,此时抛物线的开口向下,顶点坐标为(4,8);当4<t≤8时,直接根据三角形面积公式得到S=
(t﹣4)2+8,此时抛物线的开口向下,顶点坐标为(4,8);当4<t≤8时,直接根据三角形面积公式得到S=![]() (8﹣t)2=
(8﹣t)2=![]() (t﹣8)2,此时抛物线开口向上,顶点坐标为(8,0),于是根据这些特征可对四个选项进行判断.
(t﹣8)2,此时抛物线开口向上,顶点坐标为(8,0),于是根据这些特征可对四个选项进行判断.
解:当0≤t≤4时,S=S正方形ABCD﹣S△ADF﹣S△ABE﹣S△CEF
=44﹣![]() 4(4﹣t)﹣
4(4﹣t)﹣![]() 4(4﹣t)﹣
4(4﹣t)﹣![]() tt
tt
=﹣![]() t2+4t
t2+4t
=﹣![]() (t﹣4)2+8;
(t﹣4)2+8;
当4<t≤8时,S=![]() (8﹣t)2=
(8﹣t)2=![]() (t﹣8)2.
(t﹣8)2.
故选D.

练习册系列答案
相关题目