题目内容
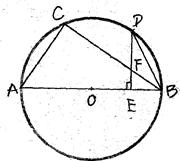
(8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交
半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
(1)解:∵点C时OA的中点,∴OC=![]() OA=
OA=![]() OD
OD
∵CD⊥OA,∴∠OCD=90°。
在Rt△OCD中,cos∠COD=![]()
∴∠COD=60°,即∠AOD=60°。
(2)证明:连结OE,∵点E是的中点,
∴![]() ,
,
∴∠BOE=∠DOE=![]() ∠DOB=
∠DOB= (180°-∠COD)=
(180°-∠COD)=![]() (180°-60°)=60°。
(180°-60°)=60°。
∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°
∴∠EAO=30°,
∴PD∥AE,
∴∠P=∠EAO=30°。
由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,
∴PD是半圆O的切线。
解析:略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 ,∠COD=60°.
,∠COD=60°.

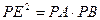 .
.
 于D.
于D.
 ,DE⊥AB于E,交BC于F. 已知AC=6,⊙O的半径是5.
,DE⊥AB于E,交BC于F. 已知AC=6,⊙O的半径是5.