题目内容
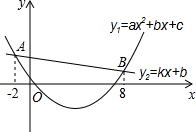已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=mx+n（m≠0）的图象相交于点A（-2，4），B（8，2），如图所示，则能使y1＜y2成立的x的取值范围是________．
-2＜x＜8
分析：根据图象，找出二次函数图象在一次函数图象下方的部分的x的取值范围即可．
解答：由图形可得，当-2＜x＜8时，二次函数图象在一次函数图象下方，y1＜y2，
所以，使y1＜y2成立的x的取值范围是-2＜x＜8．
故答案为：-2＜x＜8．
点评：本题考查了二次函数与不等式，根据函数图象求不等式的解，关键在于认准在上方与下方的函数图象所对应的函数解析式，数形结合是数学中的重要思想之一．
分析：根据图象，找出二次函数图象在一次函数图象下方的部分的x的取值范围即可．
解答：由图形可得，当-2＜x＜8时，二次函数图象在一次函数图象下方，y1＜y2，
所以，使y1＜y2成立的x的取值范围是-2＜x＜8．
故答案为：-2＜x＜8．
点评：本题考查了二次函数与不等式，根据函数图象求不等式的解，关键在于认准在上方与下方的函数图象所对应的函数解析式，数形结合是数学中的重要思想之一．
练习册系列答案
相关题目
已知二次函数y1=x2-2x-1的图象和反比例函数
如图，已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A（-2，4），B（8，2），则能使y1＜y2成立的x的取值范围是
（2013•吴江市模拟）如图，已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于A（-1，2）、B（4，1）两点，则关于x的不等式ax2+bx+c＞kx+m的解集是
已知二次函数y1=ax2+bx-3的图象经过点A（2，-3），B（-1，0），与y轴交于点C，与x轴另一交点交于点D．