题目内容
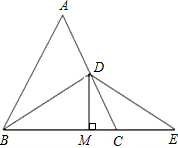 如图所示,已知,如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,又DM⊥BC,AB=10cm.
如图所示,已知,如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,又DM⊥BC,AB=10cm.(1)求BE的长;
(2)求证:BM=EM.
分析:求BE的长,即BC与CE的和,AB=10,所以BC=10,因为CE=CD,CD=
AC,可求BE的长.第二问中由(1)可求∠E=∠BDC=30°,得出BD=DE,因为DM⊥BC,进而可证明两线段相等.
| 1 |
| 2 |
解答:(1)解:∵△ABC是等边三角形,
∴AB=AC=BC=10cm
又∵D是AC的中点,
∴CD=
AC=5cm
又∵CD=CE
∴CE=5cm
BE=BC+CE=10+5=15cm;
证明:(2)∵△ABC是等边三角形,
D是AC的中点,
∴BD平分∠ABC(三线合一),
∴∠ABC=2∠DBE.∵CE=CD,
∴∠CED=∠CDE.
又∵∠ACB=∠CED+∠CDE,
∴∠ACB=2∠E.
又∵∠ABC=∠ACB,
∴2∠DBC=2∠E,
∴∠DBC=∠E,
∴BD=DE.
又∵DM⊥BE,
∴BM=EM.
或(2)证明:
∵在等边△ABC中,BD是中线
∴BD⊥AC,∠ACB=60°
∴∠DBC=30°
又∵CE=CD
∴∠E=∠CDE=
∠ACB=30°
∴∠DBC=∠E
∴BD=DE
又∵BM⊥BE
∴BM=EM.
∴AB=AC=BC=10cm
又∵D是AC的中点,
∴CD=
| 1 |
| 2 |
又∵CD=CE
∴CE=5cm
BE=BC+CE=10+5=15cm;
证明:(2)∵△ABC是等边三角形,
D是AC的中点,
∴BD平分∠ABC(三线合一),
∴∠ABC=2∠DBE.∵CE=CD,
∴∠CED=∠CDE.
又∵∠ACB=∠CED+∠CDE,
∴∠ACB=2∠E.
又∵∠ABC=∠ACB,
∴2∠DBC=2∠E,
∴∠DBC=∠E,
∴BD=DE.
又∵DM⊥BE,
∴BM=EM.
或(2)证明:
∵在等边△ABC中,BD是中线
∴BD⊥AC,∠ACB=60°
∴∠DBC=30°
又∵CE=CD
∴∠E=∠CDE=
| 1 |
| 2 |
∴∠DBC=∠E
∴BD=DE
又∵BM⊥BE
∴BM=EM.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得∠DBC=∠E是正确解答本题的关键.

练习册系列答案
相关题目
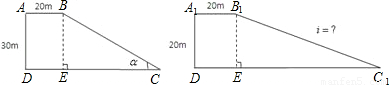
一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求.试求出改造后坡面的坡度是多少?


一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求.试求出改造后坡面的坡度是多少?


一段路基的横断面是直角梯形,如左下图所示,已知原来坡面的坡角α的正弦值为0.6,现不改变土石方量,全部利用原有土石方进行坡面改造,使坡度变小,达到如右下图所示的技术要求.试求出改造后坡面的坡度是多少?