题目内容
四边形ABCD与四边形A1B1C1D1相似，相似比为2：3，四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为5：4，则四边形ABCD与四边形A2B2C2D2相似且相似比为
- A.5：6
- B.6：5
- C.5：6或6：5
- D.8：15
A
分析：首先将2：3转化为10：15，将5：4转化为15：12，然后求得四边形ABCD与四边形A2B2C2D2相似比即可．
解答：∵四边形ABCD与四边形A1B1C1D1相似，相似比为2：3，
即：相似比为：10：15；
四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为5：4，即：15：12；
∴四边形ABCD与四边形A2B2C2D2且相似比为10：12，
也就是 5：6．
故选A．
点评：本题考查了相似多边形的性质，解题的关键是将相似比进行转换．
分析：首先将2：3转化为10：15，将5：4转化为15：12，然后求得四边形ABCD与四边形A2B2C2D2相似比即可．
解答：∵四边形ABCD与四边形A1B1C1D1相似，相似比为2：3，
即：相似比为：10：15；
四边形A1B1C1D1与四边形A2B2C2D2相似，相似比为5：4，即：15：12；
∴四边形ABCD与四边形A2B2C2D2且相似比为10：12，
也就是 5：6．
故选A．
点评：本题考查了相似多边形的性质，解题的关键是将相似比进行转换．
练习册系列答案
单元加期末复习先锋大考卷系列答案
出彩同步大试卷系列答案
相关题目
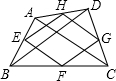如图，已知凸四边形ABCD的两对角线BD与AC之比为k，菱形EFGH各顶点位于四边形ABCD的顺次四边之上，且EF∥AC，FG∥BD，则四边形ABCD与菱形EFGH的面积之比为
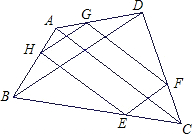在四边形ABCD中，AC、BD是四边形ABCD的两条对角线，点E、F、G、H分别是在四边形ABCD的四边上的动点，但E、F、G、H不与A、B、C、D重合，且EF∥BD∥GH，FG∥AC∥HE．
11、如图，延长四边形ABCD的四边分别至E、F、G、H，使AB=nBE，BC=nCF，CD=nDG，DA=nAH（n＞0），则四边形EFGH与四边形ABCD的面积之比为
