Question

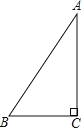
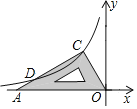
【题目】如图，把一块含30°角的三角板的直角顶点放在反比例函数y=-（x＜0）的图象上的点C处，另两个顶点分别落在原点O和x轴的负半轴上的点A处，且∠CAO=30°，则AC边与该函数图象的另一交点D的坐标为__________．

Answer 1

【答案】（-3，）

【解析】

过点C作CE⊥AO于点E，由题意可得：AE=CE，CE=OE，设点C坐标为（a，-a），代入解析式可求a=-1，可求点A坐标，点C坐标，即可求直线AC解析式，直线AC解析式与反比例函数解析式组成方程组，可求点D坐标．

如图：过点C作CE⊥AO于点E

∵∠CAO=30°，CE⊥AO
∴∠COE=60°，AC=2CE，AE=CE
∴CE=EO
设点C坐标为（a，-a）
∵点C在反比例函数y=-（x＜0）的图象上
∴a×（-a）=-
解得：a=-1，a=1（舍去）
∴点C坐标（-1，）
∴CE=，EO=1
∴AE=×=3
∴AO=4
∴点A（-4，0）
∵点A（-4，0），点C（-1，）
∴直线AC解析式y=x+
∵直线AC与反比例函数y=-相交于点C，点D
∴-=x+
解得：x1=-1，x2=-3
∴点D坐标为（-3，）
故答案为：（-3，）．