题目内容
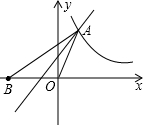 如图,已知点A是一次函数y=x+1与反比例函数y=
如图,已知点A是一次函数y=x+1与反比例函数y=| 2 | x |
分析:欲求OAB的面积,已知点A是一次函数y=x+1的图象与反比例函数y=
的图象在第一象限内的交点,可求出点A的坐标,从而得到△AOB的高,结合已知OA=OB,求得底边OB,从而求出面积.
| 2 |
| x |
解答:解:依题意A点的坐标满足方程组
∴
∴A(1,2)
∴OA=
∵OB=OA=
∴S△AOB=
OB×2=
×2×
=
.
故答案为:
.
|
∴
|
∴A(1,2)
∴OA=
| 5 |
∵OB=OA=
| 5 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
故答案为:
| 5 |
点评:此题主要考查反比例函数的性质,注意通过解方程组求出交点坐标.同时要注意运用数形结合的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
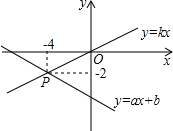 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( )
六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.按照这样的规定,每掷一次该小立方体,就得到平面内的一个点的坐标.已知小明前两次掷得的两个点能确定一条直线,且这条直线经过点P(4,7),那么他第三次掷得的点也在直线上的概率是( ) 你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么?
你结合这个新的图象回答:当直线y=x+m(m<1)与此图象有两个公共点时,m的取值范围是什么? 如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组
如图,已知函数y=ax+b和y=kx的图象交于点P,则二元一次方程组