题目内容
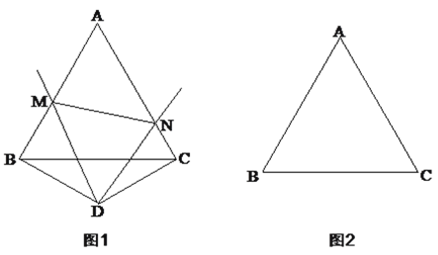
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是边
是边![]() 的中点,连接
的中点,连接![]() 延长与
延长与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
(![]() )求证:四边形
)求证:四边形![]() 是平行四边形.
是平行四边形.
(![]() )已知
)已知![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(![]() )证明见解析;(
)证明见解析;(![]() )
)![]()
![]() .
.
【解析】试题分析:
(1)由![]() 可证得
可证得![]() ,由此可得
,由此可得![]() ,结合
,结合![]() ,
,![]() ,可证得
,可证得![]() ≌
≌![]() ,即可得到
,即可得到![]() 结合DE=CE即可证得四边形BDFC是平行四边形;
结合DE=CE即可证得四边形BDFC是平行四边形;
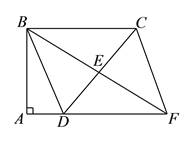
(2)过点D作DH⊥BC于点H,易证四边形ADHB是矩形,从而可得BH=AD=1,结合BC=3可得CH=2,在Rt△DHC中结合CD=BC=3即可求得DH=![]() ,这样即可求得四边形BDFC的面积了.
,这样即可求得四边形BDFC的面积了.
试题解析:
(![]() )∵
)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
(![]() )过
)过![]() 作
作![]() 于
于![]() ,
,
∴∠DHB=∠A=∠ABH=90°,
∴四边形ADHB是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目