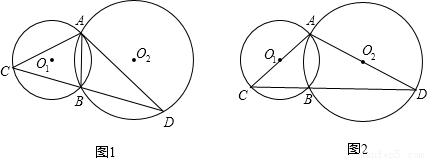Question

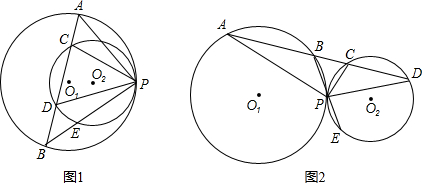
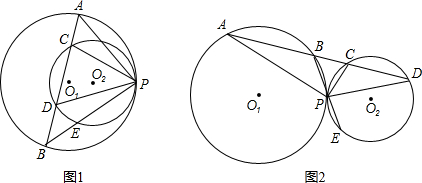
如图1，已知⊙O₁与⊙O₂相交于点A、B，且半径分别为2和3．过A任意作⊙O₁中的弦AC，连接CB并延长交⊙O₂于点D，连接AD．
（1）若AC是⊙O₁的直径（如图2），求证：AD也是⊙O₂的直径；
（2）求图1中的AC与AD的比值是否为定值？若是，请求出这个值；若不是，请说明理由．

Answer 1

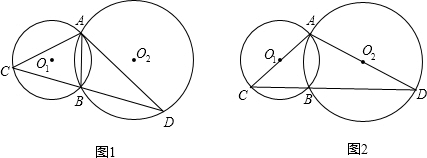
分析：（1）欲证AD也是⊙O₂的直径；根据直径所对的圆周角为直角，90°的圆周角所对的弦为直径，只需证明∠ABD=90°即可．
（2）求图1中的AC与AD的比值，先过点A作⊙O₁的直径AE，连接EB并延长交⊙O₂于点F；连接AF、CE、DF，证明△CAE∽△DAF，得出比例关系式即可．

解答：解：（1）∵AC是⊙O₁的直，
∴∠ABC=90°．
∴∠ABD=90°．
∴AD是⊙O₂的直径．（6分）

（2）AC与AD的比值是定值

2

3

（8分）
过点A作⊙O₁的直径AE，连接EB并延长交⊙O₂于点F，
连接AF、CE、DF，
由（1）可知：AF是⊙O₂的直径，∠ABE=∠ABF=90°，
∵∠CAE=∠CBE，∠DAF=∠DBF，
又∵∠CBE=∠DBF，
∴∠CAE=∠DAF．
∴△CAE∽△DAF．
∴

AC

AD

=

AE

AF

=

4

6

=

2

3

．
∴AC与AD的比值是定值

2

3

．（14分）

点评：本题考查圆周角的应用能力，熟悉直径所对的圆周角为直角，90°的圆周角所对的弦为直径的知识，同时考查了相似三角形的性质．