题目内容
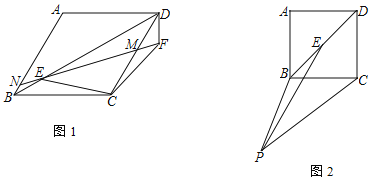
【题目】点A、C为半径是8的圆周上两动点，点B为
的中点，以线段BA、BC为邻边作菱形ABCD，顶点D恰在该圆半径的中点上，则该菱形的边长为_____．
【答案】
或
【解析】
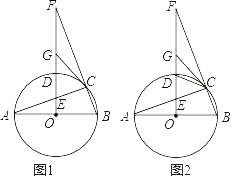
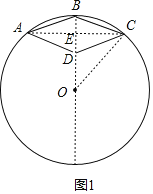
过B作直径，连接AC交BO于E，如图①，根据已知条件得到BD=
OB=4，求得OD、OE、DE的长，连接OC，根据勾股定理得到结论；如图②，BD=12，求得OD、OE、DE的长，连接OD，根据勾股定理得到结论．
过B作直径，连接AC交BO于E，
∵点B为
的中点，
∴BD⊥AC，
如图①，
∵点D恰在该圆直径上，D为OB的中点，
∴BD=×8=4，
∴OD=OB-BD=4，
∵四边形ABCD是菱形，
∴DE=BD=2，
∴OE=2+4=6，
连接OC，
∵CE=
，
在Rt△DEC中，由勾股定理得：DC=
；
如图②，
OD=4，BD=8+4=12，DE=BD=6，OE=6-4=2，
由勾股定理得：CE=
，
DC=
，
故答案为：或．
一本好题口算题卡系列答案
【题目】为了弘扬我国古代数学发展的伟大成就，某校九年级进行了一次数学知识竞赛，并设立了以我国古代数学家名字命名的四个奖项：“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”，根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图，并得到了获“祖冲之奖”的学生成绩统计表：
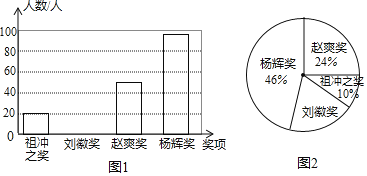
“祖冲之奖”的学生成绩统计表：
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息，解答下列问题：
这次获得“刘徽奖”的人数是多少，并将条形统计图补充完整；
获得“祖冲之奖”的学生成绩的中位数是多少分，众数是多少分；
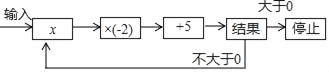
在这次数学知识竟赛中有这样一道题：一个不透明的盒子里有完全相同的三个小球，球上分别标有数字“
”，“
”和“2”，随机摸出一个小球，把小球上的数字记为x放回后再随机摸出一个小球，把小球上的数字记为y，把x作为横坐标，把y作为纵坐标，记作点
用列表法或树状图法求这个点在第二象限的概率．
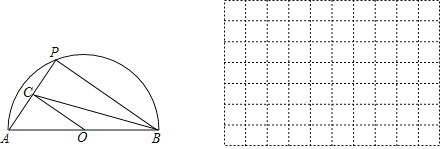
【题目】如图，P是半圆弧
上一动点，连接PA、PB，过圆心O作
交PA于点C，连接
已知
，设O，C两点间的距离为xcm，B，C两点间的距离为ycm．
小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行探究．
下面是小东的探究过程，请补充完整：
通过取点、画图、测量，得到了x与y的几组值，如下表：
| 0 |
| 1 |
| 2 |
| 3 |
| 3 |
|
|
|
| 6 |
说明：补全表格时相关数据保留一位小数
建立直角坐标系，描出以补全后的表中各对应值为坐标的点，画出该函数的图象；
结合画出的函数图象，解决问题：直接写出
周长C的取值范围是______．
