题目内容
下列命题中,错误的一个是
- A.如果a、b互为相反数,那么a+1和b-1仍是互为相反数
- B.不论x是什么实数,x2-2x+
 的值总是大于0
的值总是大于0 - C.n是自然数,
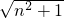 一定是一个无理数
一定是一个无理数 - D.如果
 是一个无理数,那么a是非完全平方数
是一个无理数,那么a是非完全平方数
C
分析:A、根据实数的相反数的定义即可判定;
B、根据实数的性质利用代数变形即可判定;
C、根据算术平方根的定义和自然数的性质即可判定;
D、根据算术平方根的定义和有理数的性质即可判定.
解答:A、如果a、b互为相反数,则有a+b=0,那么a+1+b-1=0,所以a+1和b-1仍是互为相反数,故选项正确;
B、因为x2-2x+ =(x-1)2+
=(x-1)2+ >0,所以不论x是什么实数,x2-2x+
>0,所以不论x是什么实数,x2-2x+ 的值总是大于0,故选项正确;
的值总是大于0,故选项正确;
C、当n=0时,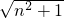 =1是一个有理数,故选项错误;
=1是一个有理数,故选项错误;
D、如果 是一个无理数,那么a是非完全平方数,故选项正确.
是一个无理数,那么a是非完全平方数,故选项正确.
故选C.
点评:本题主要考查了相反数,无理数的概念以及它们实际运用.解题时要会灵活的把各知识点综合应用,尤其要会举出反例来证明题中结论的错误性.
分析:A、根据实数的相反数的定义即可判定;
B、根据实数的性质利用代数变形即可判定;
C、根据算术平方根的定义和自然数的性质即可判定;
D、根据算术平方根的定义和有理数的性质即可判定.
解答:A、如果a、b互为相反数,则有a+b=0,那么a+1+b-1=0,所以a+1和b-1仍是互为相反数,故选项正确;
B、因为x2-2x+
 =(x-1)2+
=(x-1)2+ >0,所以不论x是什么实数,x2-2x+
>0,所以不论x是什么实数,x2-2x+ 的值总是大于0,故选项正确;
的值总是大于0,故选项正确;C、当n=0时,
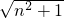 =1是一个有理数,故选项错误;
=1是一个有理数,故选项错误;D、如果
 是一个无理数,那么a是非完全平方数,故选项正确.
是一个无理数,那么a是非完全平方数,故选项正确.故选C.
点评:本题主要考查了相反数,无理数的概念以及它们实际运用.解题时要会灵活的把各知识点综合应用,尤其要会举出反例来证明题中结论的错误性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目