题目内容
一个圆锥的侧面展开图形是半径为8cm，圆心角为120°的扇形，则此圆锥的底面半径为
- A.
cm - B.
cm - C.3cm
- D.
cm
A
分析：利用弧长公式和圆的周长公式求解．
解答：设此圆锥的底面半径为r，
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得：
2πr=
，
r=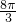
cm．
故选A．
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
分析：利用弧长公式和圆的周长公式求解．
解答：设此圆锥的底面半径为r，
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得：
2πr=
，r=
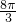cm．故选A．
点评：圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
练习册系列答案
相关题目
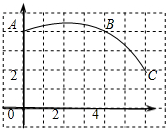如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
（2013•本溪二模）一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是
如图，一个圆锥的侧面展开图是90°的扇形．
如图，在单位长度为1的正方形网格中建立平面直角坐标系，一段圆弧经过网格的交点为A、B、C．