Question

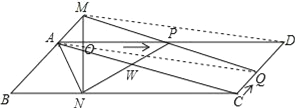
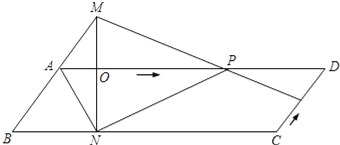
【题目】已知：如图，ABCD中，AD=3cm，CD=1cm，∠B=45°，点P从点A出发，沿AD方向匀速运动，速度为3cm/s；点Q从点C出发，沿CD方向匀速运动，速度为1cm/s，连接并延长QP交BA的延长线于点M，过M作MN⊥BC，垂足是N，设运动时间为t（s）（0＜t＜1）．

（1）当t为何值时，四边形AQDM是平行四边形？

（2）证明：在P、Q运动的过程中，总有CQ=AM；

（3）是否存在某一时刻t，使四边形ANPM的面积是平行四边形ABCD的面积的一半？若存在，求出相应的t值；若不存在，说明理由．

Answer 1

【答案】(1) 是 (2)见解析 (3) 当t= s时，四边形ANPM的面积是平行四边形ABCD的面积的一半

【解析】试题分析: （1）连结AQ、MD，根据平行四边形的对角线互相平分得出AP=DP，代入求出即可；

（2）根据已知得出△AMP∽△DQP，再根据相似三角形的性质得出=，求出AM的值，从而得出在P、Q运动的过程中，总有CQ=AM；

（3）根据已知条件得出BN=MN，再根据BM=AB+AM，由勾股定理得出BN=MN=（1+t），根据四边形ABCD是平行四边形，得出MN⊥AD，设四边形ANPM的面积为y，得出y=×AP×MN，假设存在某一时刻t，四边形ANPM的面积是平行四边形ABCD的面积的一半，得出t2+t=×3×，最后进行整理，即可求出t的值．

试题解析:

（1）连结AQ、MD，

∵当AP=PD时，四边形AQDM是平行四边形，

∴3t=3﹣3t，

解得：t=，

∴t=s时，四边形AQDM是平行四边形．

（2）∵四边形ABCD是平行四边形，

∴AB∥CD，

∴△AMP∽△DQP，

∴=，

∴=，

∴AM=t，

即在P、Q运动的过程中，总有CQ=AM；

（3）∵MN⊥BC，

∴∠MNB=90°，

∵∠B=45°，

∴∠BMN=45°=∠B，

∴BN=MN，

∵BM=AB+AM=1+t，

在Rt△BMN中，由勾股定理得：BN=MN=（1+t），

∵四边形ABCD是平行四边形，

∴AD∥BC，

∵MN⊥BC，

∴MN⊥AD，

设四边形ANPM的面积为y，

∴y=×AP×MN=×3t×（1+t）=t2+t（0＜t＜1）．

假设存在某一时刻t，四边形ANPM的面积是平行四边形ABCD的面积的一半，

∴t2+t=×3×，

整理得：t2+t﹣1=0，

解得：t1=，t2=（舍去），

∴当t=s时，四边形ANPM的面积是平行四边形ABCD的面积的一半．