题目内容
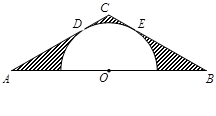
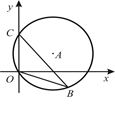
如图,在△ABC中, AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
小题1:求半圆O的半径;
小题2:求图中阴影部分的面积.
 AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
AC="BC," AB=6,O为AB的中点,且以O为圆心的半圆与AC,BC分别相切于点D,E;
小题1:求半圆O的半径;
小题2:求图中阴影部分的面积.
小题1:解:连结OD,OC,

∵半圆与AC,BC分别相切于点D,E.
∴
 .
.∵
 ,且O是AB的中点.∴
,且O是AB的中点.∴
∴.AO=
 AB=3
AB=3∵
 ,∴
,∴ .
.∴
 .
.∴在
 中,.OD=
中,.OD= AO=
AO=
即半圆的半径为
 .
. 小题2:设CO=x,则在
 中,因为
中,因为 ,所以AC=2x,由勾股定理得:
,所以AC=2x,由勾股定理得:
即
 (2x)
(2x) -x
-x =3
=3
解得 x=
 (x=-
(x=- 舍去)
舍去)S=
 ×6×
×6× -
- ×π×(
×π×( )
) =3
=3 -
- π
π ∴阴影部分的面积为3
 -
- π
π分析:(1)连接OC,OD,根据切线的性质得到OD⊥AC,在直角△AOD中,用30°角所对的直角边等于斜边的一半,可以求出半圆的半径.
(2)先在直角△AOC中求出OC的长,计算出△ABC的面积,然后用三角形的面积减去半圆的面积得到阴影部分的面积.
解:连结OD,OC,

∵半圆与AC,BC分别相切于点D,E.
∴ .
.
∵ ,且O是AB的中点.∴
,且O是AB的中点.∴
∴.AO= AB=3
AB=3
∵ ,∴
,∴ .
.
∴ .
.
∴在 中,.OD=
中,.OD= AO=
AO=
即半圆的半径为 .
.
小题2:设CO=x,则在 中,因为
中,因为 ,所以AC=2x,由勾股定理得:
,所以AC=2x,由勾股定理得:

即 (2x)
(2x) -x
-x =3
=3
解得 x= (x=-
(x=- 舍去)
舍去)
S= ×6×
×6× -
- ×π×(
×π×( )
) =3
=3 -
- π
π
∴阴影部分的面积为3 -
- π
π
(2)先在直角△AOC中求出OC的长,计算出△ABC的面积,然后用三角形的面积减去半圆的面积得到阴影部分的面积.
解:连结OD,OC,

∵半圆与AC,BC分别相切于点D,E.
∴
 .
.∵
 ,且O是AB的中点.∴
,且O是AB的中点.∴
∴.AO=
 AB=3
AB=3∵
 ,∴
,∴ .
.∴
 .
.∴在
 中,.OD=
中,.OD= AO=
AO=
即半圆的半径为
 .
. 小题2:设CO=x,则在
 中,因为
中,因为 ,所以AC=2x,由勾股定理得:
,所以AC=2x,由勾股定理得:
即
 (2x)
(2x) -x
-x =3
=3
解得 x=
 (x=-
(x=- 舍去)
舍去)S=
 ×6×
×6× -
- ×π×(
×π×( )
) =3
=3 -
- π
π ∴阴影部分的面积为3
 -
- π
π
练习册系列答案
相关题目


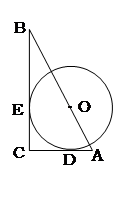
 .
.
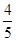
 A.50° B.80° C.100° D.200°
A.50° B.80° C.100° D.200°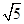 cm
cm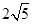 cm
cm