题目内容
 已知直线l:y=
已知直线l:y=| 1 |
| 2 |
(Ⅰ)用含a的代数式表示c.
(Ⅱ)抛物线在A,B之间的部分(不包含点A,B)记为图形G,请结合函数图象解答:若图形G在直线l下方,求a的取值范围.
考点:二次函数的性质
专题:计算题
分析:(1)先利用一次函数解析式求出A点坐标为(-2,0),然后把A点坐标代入抛物线解析式即可得到a与c的关系式;
(2)先分别计算出x=4时所对应的一次函数值和二次函数值,然后利用图形G在直线l下方得到12-12a≤3,然后解不等式即可.
(2)先分别计算出x=4时所对应的一次函数值和二次函数值,然后利用图形G在直线l下方得到12-12a≤3,然后解不等式即可.
解答: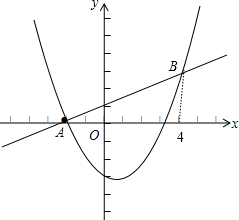 解:(Ⅰ)当y=0时,
解:(Ⅰ)当y=0时,
x+1=0,解得x=-2,则A点坐标为(-2,0),
把A(-2,0)代入y=ax2-2x+c得4a+4+c=0,
所以c=-4a-4;
(Ⅱ)当x=4时,y=ax2-2x+c=16a-8-4a-4=12a-12,则B(4,12a-12),
当x=4时,y=
x+1=3,
因为图形G在直线l下方,
所以12-12a≤3,
解得a≤
,
所以a的取值范围为0<a≤
.
 解:(Ⅰ)当y=0时,
解:(Ⅰ)当y=0时,| 1 |
| 2 |
把A(-2,0)代入y=ax2-2x+c得4a+4+c=0,
所以c=-4a-4;
(Ⅱ)当x=4时,y=ax2-2x+c=16a-8-4a-4=12a-12,则B(4,12a-12),
当x=4时,y=
| 1 |
| 2 |
因为图形G在直线l下方,
所以12-12a≤3,
解得a≤
| 5 |
| 4 |
所以a的取值范围为0<a≤
| 5 |
| 4 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
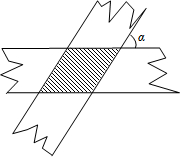 如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )
如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|
(x2+ax+8)(x2-3x+b)展开式中不含x3和x2项,则a、b的值分别为( )
| A、a=3,b=1 |
| B、a=-3,b=1 |
| C、a=0,b=0 |
| D、a=3,b=8 |
已知关于x的方程ax-8=20+a的解是x=-3,则a的值为( )
| A、-4 | B、-6 | C、-7 | D、-3 |
 如图,
如图,
 用含m,n的代数式表示图中阴影部分的面积是
用含m,n的代数式表示图中阴影部分的面积是 如图,已知P、M、N三点,按下面要求画出图形;
如图,已知P、M、N三点,按下面要求画出图形;