题目内容
【题目】我们知道1+2+3+…+
=
，则1+2+3+…+10＝ ___________ .
[问题提出] 那么 
的结果等于多少呢？
[阅读理解] 在图1所示的三角形数阵中，第1行圆圈中的数为1，即12 ；第2行两个圆圈中数的和为2+2，即22；......；第n行n个圆圈中数的和为n+n+
n即 n2；这样，该三角形数阵中共有____ 个圆圈，所有圆圈中数的和可表示为_________________ .
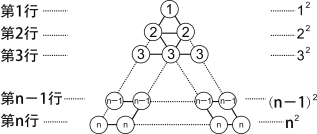
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第n－1行的第一个圆圈中的数分别为n－1，2，n）发现每个位置上三个圆圈中的数的和均为______________.由此可得，这三个三角形数阵所有圆圈中数的总和为：
3（ ）＝_________________.因此， ＝__________.
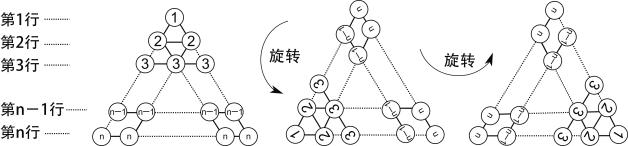
图2
[问题解决]
（1）.根据以上规律可得
__________________.
（2）.试计算 
，请写出计算步骤.
【答案】55；
；
；（
）；
；
；（1）7；（2）2485
【解析】
把n=10代入1+2+3+…+
=，即可求出1+2+3+…+10的值；
[阅读理解]：由图1可知，共有1+2+3+…+n=个圆圈，所有圆圈中数的和可表示为；
[规律探究]：由图2知，每个位置上三个圆圈中的数的和均为.由此可得，这三个三角形数阵所有圆圈中数的总和为：3（
）＝每个位置上三个圆圈中的数的和（）×位置的个数，因此， ＝；
[问题解决]：（1）先化简把
，然后把n=10代入就算即可；（2）用（
）减去（
）即可求出结论.
当n=10时，
1+2+3+…+
=
=55；
[阅读理解]：由图1可知，共有1+2+3+…+n=个圆圈，所有圆圈中数的和可表示为；
[规律探究]：由图2知，每个位置上三个圆圈中的数的和均为.由此可得，这三个三角形数阵所有圆圈中数的总和为：3（ ）＝，因此， ＝；
[问题解决]：（1）∵
，
把n=10代入得，
原式=
=7；
（2）
=（）-（）
=
=
=2485.
