Question

【题目】在平面直角坐标系xOy中，点A（x，0），B（x，y），若线段AB上存在一点Q满足，则称点Q是线段AB的“倍分点”．

（1）若点A（1，0），AB＝3，点Q是线段AB的“倍分点”．

①求点Q的坐标；

②若点A关于直线y＝x的对称点为A′，当点B在第一象限时，求；

（2）⊙T的圆心T（0，t），半径为2，点Q在直线y＝ x上，⊙T上存在点B，使点Q是线段AB的“倍分点”，直接写出t的取值范围．

Answer 1

【答案】（1）①Q（1，1）或Q'（1，﹣1），②；（2）t的取值范围为﹣4≤t≤4

【解析】

(1) ①根据 “倍分点”的定义及A（1，0），AB＝3，可得Q的坐标；②点A（1，0）关于直线y＝x的对称点为A′（0，1），可得QA＝QA′，可得答案；

(2)分①当A，B都在⊙T1上时，可得t的值，②当⊙T2上只有一个点Q是线段AB的“倍分点”时，过点T2作T2Q⊥图象L于点Q，交⊙T2于点N，过点Q作QD⊥x轴于点D，可得t的取值范围.

解：（1）如图1，

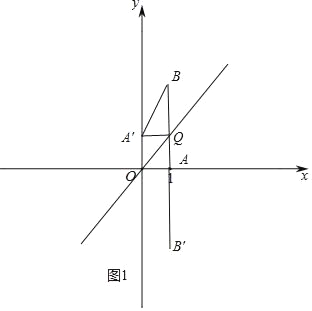
∵A（1，0），AB＝3

∴B（1，3）或B'（1，﹣3）

∵

∴Q（1，1）或Q'（1，﹣1）

（2）点A（1，0）关于直线y＝x的对称点为A′（0，1），如图1，

∴QA＝QA′

∴，

（3）①当A，B都在⊙T1上时，⊙T1与L没有交点，

∵⊙T1的半径为2，

∴此时点T1的坐标为（0，﹣4）；

②当⊙T2上只有一个点Q是线段AB的“倍分点”时，过点T2作T2Q⊥图象L于点Q，交⊙T2于点N，过点Q作QD⊥x轴于点D，

∵图象L的解析式为y＝x（x＞0），

∴∠QOT＝60°，∠OT2Q＝30°．

∵点T2的坐标为（0，t），

∴OQ＝t，DQ＝OQ＝t，T2O＝t．

由“倍分点”的定义可知：OB＝2DQ，即t﹣2＝t，

解得：t＝4，

综上所述：t的取值范围为﹣4≤t≤4．