Question

【题目】已知点A（1，0）、点B（5，0），点P是该直角坐标系内的一个动点．若点P在y轴的负半轴上，且∠APB＝30°，则满足条件的点P的坐标为_____．

Answer 1

【答案】(0，﹣2﹣)或(0，﹣2+)

【解析】

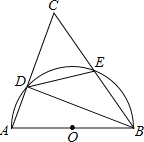
利用圆周角定理可判断点A、B、P在以C点为圆心，CA为半径的圆上，且∠ACB＝2∠APB＝60°，则CA＝CB＝AB＝4，⊙C交y轴于P和P′点，连接CP，如图，作CD⊥AB于D，CE⊥y轴于E，根据垂径定理得到得到AD＝DB＝2，PE＝P′E，所以CD＝2，OA＝3，再利用勾股定理计算出PE得到OP′和OP的长，从而得到满足条件的点P的坐标．

解：∵∠APB＝30°，

∴点A、B、P在以C点为圆心，CA为半径的圆上，且∠ACB＝2∠APB＝60°，

∴△ABC为等边三角形，

∴CA＝CB＝AB＝4，

设⊙C交y轴于P和P′点，连接CP，如图，

作CD⊥AB于D，CE⊥y轴于E，则AD＝DB＝2，PE＝P′E，

∵∠BOP=90°，

∴四边形OECD是矩形，

∴OE=CD，OD=CE.

∵AD＝2，CA＝4，

∴CD＝2，OD＝OA+AD＝3，

在Rt△PCE中，PE＝=，

∵OE＝CD＝2，

∴OP′＝2﹣，OP＝2+，

∴P（0，﹣2﹣），P′（0，﹣2+），

∴满足条件的点P的坐标为（0，﹣2﹣）或（0，﹣2+）．

故答案为（0，﹣2﹣）或（0，﹣2+）．