Question

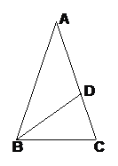
【题目】如图，已知△ABC中，D是AC边上一点，∠A=36，∠C=72，∠ADB=108。

求证：(1)AD=BD=BC；

(2)点D是线段AC的黄金分割点。

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）根据三角形的内角和是180度，和题中给出的角的度数，可求得各角的度数，从而得出AD=BD=BC．（2）利用三角形的相似来证明点D是线段AC的黄金分割点．

（1）∵∠A=36°，∠C=72°，
∴∠ABC=72°，∠ADB=108°，
∴∠ABD=36°，
∴△ADB、△BDC是等腰三角形，

∴AD=BD=BC．

（2）∵∠DBC=∠A=36°，∠C=∠C，
∴△ABC∽△BDC，
∴BC：AC=CD：BC，
∴=ACDC，
∵BC=AD，
∴=ACDC，
∴点D是线段AC的黄金分割点．