题目内容
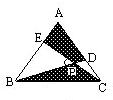 在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=
在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=60°
60°
.分析:根据可以证明AD=BE,即AE=CD,即可证△ACE≌△BCD,可得∠DBC=∠ACE,根据∠BPE=∠BCE+∠DBC,∠ACE+∠BCE=60°即可求得∠BPE=∠ACB,即可解题.
解答:解:∵△ABD的面积=四边形ADPE的面积+△BPE的面积
△BCE的面积=三角形BPC的面积+△BPE的面积
四边形ADPE与△BPC的面积相等,
∴AD=BE,即AE=CD,
又∵AC=BC,∠BAC=∠ACB=60°
∴△ACE≌△BCD,
∴∠DBC=∠ACE
又∵∠BPE=∠BCE+∠DBC,∠ACE+∠BCE=60°,
∴∠BPE=∠ACB=60°,
故答案为 60°.
△BCE的面积=三角形BPC的面积+△BPE的面积
四边形ADPE与△BPC的面积相等,
∴AD=BE,即AE=CD,
又∵AC=BC,∠BAC=∠ACB=60°
∴△ACE≌△BCD,
∴∠DBC=∠ACE
又∵∠BPE=∠BCE+∠DBC,∠ACE+∠BCE=60°,
∴∠BPE=∠ACB=60°,
故答案为 60°.
点评:本题考查了三角形面积的计算,考查了等边三角形各内角为60°的性质,考查了全等三角形的证明和全等三角形对应角相等的性质,本题中求证△ACE≌△BCD是解题的关键.

练习册系列答案
相关题目
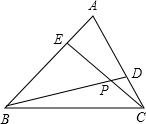 如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )
如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )| A、60° | B、45° | C、75° | D、50° |
 如图,在正△ABC中,D为BC中点,则∠BAD的度数为( )
如图,在正△ABC中,D为BC中点,则∠BAD的度数为( )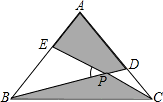 在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=________.
在正△ABC中(如图),D为AC上一点,E为AB上一点,BD,CE相交于P,若四边形ADPE与△BPC的面积相等,那么∠BPE=________.