Question

【题目】材料阅读：对于一个圆和一个正方形给出如下定义：若圆上存在到此正方形四条边距离都相等的点，则称这个圆是该正方形的“等距圆”．

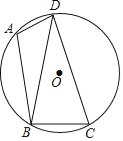
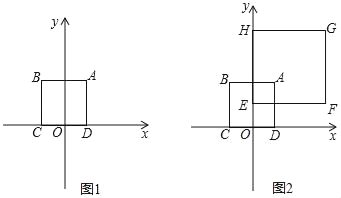
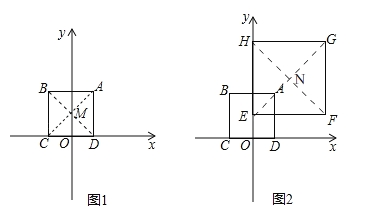
如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧．

（1）当r=2时，在P1（2，0），P2（﹣4，2），P3（2，2），P4（2﹣2，0）中可以成为正方形ABCD的“等距圆”的圆心的是　 　；

（2）若点P坐标为（﹣2，﹣1），则当⊙P的半径r=　 　时，⊙P是正方形ABCD的“等距圆”．试判断此时⊙P与直线BD的位置关系？并说明理由．

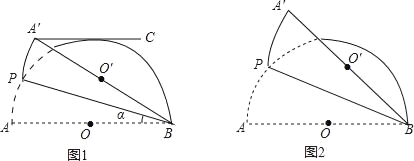
（3）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（8，2），顶点E、H在y轴上，且点H在点E的上方．若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P的圆心P的坐标．

Answer 1

【答案】(1) P1（2，0），P2（﹣2，4）或P4（0，2﹣2）；(2) 相交；(3) （，）或（，）．

【解析】分析：（1）根据“等距圆”的定义，可知只要圆经过正方形的中心，即是正方形的“等距圆”，也就是说圆心与正方形中心的距离等于圆的半径即可，从而可以判断哪个点可以成为正方形ABCD的“等距圆”的圆心，本题得以解决；

（2）根据题意可知，只要求出点P与正方形ABCD的中心的距离即可求得半径r的长度，连接PE，可以得到直线PE的解析式，看点B是否在此直线上，由BE与直线AC的关心可以判断PE与直线AC的关系，本题得以解决；

（3）根据题意，可以得到点P满足的条件，列出形应的二元一次方程组，从而可以求得点P的坐标．

详解：（1）连接AC、BD相交于点M，如右图1所示．

∵四边形ABCD是正方形，∴点M是正方形ABCD的中心，到四边的距离相等，∴⊙P一定过点M．

∵正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧，∴点M（0，2），设⊙P的圆心坐标是（x，y），∴（x﹣0）2+（y﹣2）2=（2 ）2，将P1（2，0），P2（﹣4，2），P3（2，2），P4（2﹣2，0）分别代入上面的方程，只有P1（2，0），P2（﹣2，4）和P4（0，2﹣2）成立．

故答案为：P1（2，0），P2（﹣2，4）或P4（0，2﹣2）；

（2）由题意可得： 点M的坐标为（0，2），点P（﹣2，﹣1），∴r==，即当P点坐标为（﹣2，﹣1），则当⊙P的半径r是时，⊙P是正方形ABCD的“等距圆”；

故答案为：．

此时⊙P与直线AC的位置关系是相交，理由：∵正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C在点D的左侧，∴点B（﹣2，4），D（2，0），设过点B（﹣2，4），点D（2，0）的直线的解析式为y=kx+b，则 ，解得：，即直线AC的解析式为：y=﹣x+2①，∴过点P（﹣2，﹣1）垂直于BD的直线解析式为y=x+1②，记垂足为G，联立①②，解得：G的坐标为（），∴PG=

∴点P（﹣2，﹣1）到直线BD的距离为：＜；

∴此时⊙P与直线AC的位置关系是相交；

（3）设点P的坐标为（x，y），连接HF、EG交于点N，则点N为正方形EFGH的中心，其坐标为（4，6）如图2所示．

∵点E（0，2），N（4，6），点C（﹣2，0），点B（﹣2，4），⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，∴，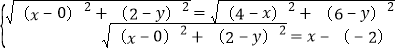

解得：或

即⊙P的圆心P的坐标是（，）或（，）．