题目内容
抛物线 交
交 轴于
轴于 两点,交
两点,交 轴于点
轴于点 ,对称轴为直线
,对称轴为直线 。且A、C两点的坐标分别为
。且A、C两点的坐标分别为 ,
,

【小题1】求抛物线 的解析式;
的解析式;
【小题2】在对称轴上是否存在一个点 ,使
,使 的周长最小.若存在,请求出点
的周长最小.若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【小题1】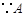 、
、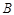 两点关于
两点关于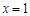 对称,且
对称,且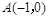 ,
,
∴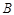 点坐标为
点坐标为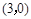 ,………………………………………………1分
,………………………………………………1分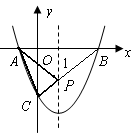
根据题意得: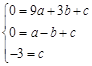
解得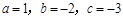 .
. 抛物线的解析式为
抛物线的解析式为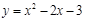 . …………………………5分
. …………………………5分
【小题2】存在一个点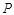 ,使
,使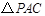 的周长最小. ………………6分
的周长最小. ………………6分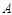 点关于
点关于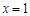 对称点
对称点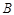 的坐标为
的坐标为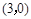 ,
,
设直线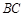 的解析式为
的解析式为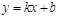

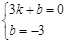

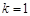 ,
,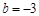 ,即
,即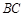 的解析式为
的解析式为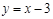 . ………………10分
. ………………10分
当 时,
时,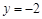 ,
, 
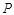 点坐标为
点坐标为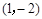 .……………………………………………12分
.……………………………………………12分
解析

练习册系列答案
相关题目
(本题满分12分)在平面直角坐标系中,抛物线交 轴于
轴于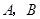 两点,交
两点,交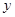 轴于点
轴于点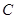 ,已知抛物线的对称轴为
,已知抛物线的对称轴为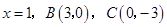 .
.
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【小题3】(3)如果在 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于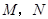 两点,以
两点,以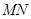 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径.
 轴于
轴于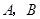 两点,交
两点,交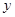 轴于点
轴于点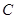 ,已知抛物线的对称轴为
,已知抛物线的对称轴为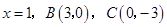 .
. |
【小题1】⑴求这个抛物线的解析式;
【小题2】⑵在抛物线的对称轴上是否存在一点
 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.【小题3】(3)如果在
 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于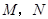 两点,以
两点,以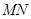 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径. 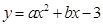 交
交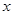 轴于
轴于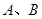 两点,交
两点,交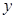 轴于点
轴于点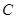 ,已知抛物线的对称轴为直线
,已知抛物线的对称轴为直线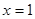 ,
,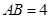 .
. ,使点
,使点 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出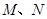 两点,若以
两点,若以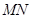 为直径的圆恰好与
为直径的圆恰好与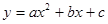 交
交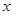 轴于
轴于 两点,交
两点,交 轴于点
轴于点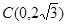 .
.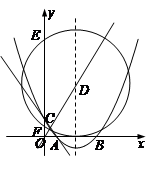
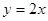 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交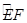 的长;
的长;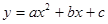 交
交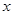 轴于
轴于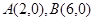 两点,交
两点,交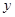 轴于点
轴于点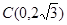 .
.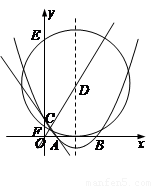
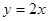 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交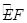 的长;
的长;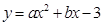 交
交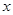 轴于
轴于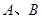 两点,交
两点,交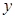 轴于点
轴于点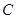 ,已知抛物线的对称轴为直线
,已知抛物线的对称轴为直线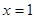 ,
,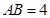 .
.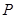 ,使点
,使点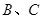 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出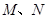 两点,若以
两点,若以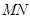 为直径的圆恰好与
为直径的圆恰好与