题目内容
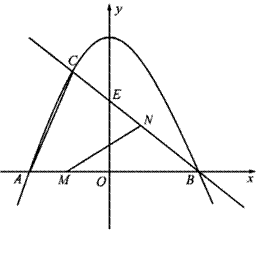
已知:如图,抛物线![]() 与
与![]() 轴的交点是
轴的交点是![]() 、
、![]() ,与
,与![]() 轴的交点是C.
轴的交点是C.
(1)求抛物线的函数表达式;
(2)设![]() (0<
(0<![]() <6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当![]() 取何值时,线段PQ的长度取得最大值?其最大值是多少?
取何值时,线段PQ的长度取得最大值?其最大值是多少?
②是否存在这样的点P,使△OAQ为直角三角 形?若存在,求出点P的坐标;若不存在,请说明理由.

解:(1)∵抛物线过A(3,0),B(6,0),
![]()
解得: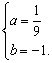
∴所求抛物线的函数表达式是![]()
(2)①∵当x=0时,y=2,
∴点C的坐标为(0,2).
设直线BC的函数表达式是![]() .
.
则有![]()
解得: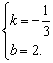
∴直线BC的函数表达式是![]() .
.
![]()
∴![]()
=![]()
=![]() .
.
∴当![]() 时,线段PQ的长度取得最大值.最大值是1.
时,线段PQ的长度取得最大值.最大值是1.
②当![]() 时,点P与点A重合,∴P(3,0)
时,点P与点A重合,∴P(3,0)
当![]() 时,点P与点C重合,∴
时,点P与点C重合,∴![]() (不合题意)
(不合题意)
当![]() 时,
时,
设PQ与![]() 轴交于点D.
轴交于点D.
![]() ,
,
![]() .
.
又![]()
∴⊿ODQ∽⊿QDA. ∴![]() ,即
,即![]() .
.
∴![]() ,
,
![]() ,∴
,∴![]() .
.
∴![]()
![]() .
.
∴![]() 或
或![]() .
.
∴所求的点P的坐标是P(3,0)或![]() 或
或![]() .
.
解法二:
当![]() 时,点P与点A重合,∴P(3,0)
时,点P与点A重合,∴P(3,0)
当![]() 时,点P与点C重合,∴
时,点P与点C重合,∴![]() (不合题意)
(不合题意)
当![]() 时,设PQ与
时,设PQ与![]() 轴交于点D.
轴交于点D.
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]()
在![]() 中,
中,![]() ,
,
∴![]() .
.
![]() ,∴
,∴![]() .
.
∴![]()
![]() .
.
∴![]() 或
或![]() .
.
∴所求的点P的坐标是P(3,0)或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案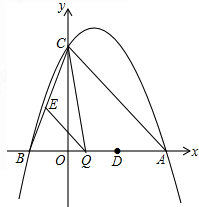 (2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).
(2012•浦江县模拟)已知:如图,抛物线与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0),点B的坐标为(-2,0).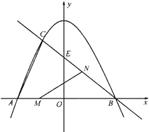
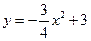 与
与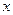 轴交于点
轴交于点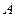 、点
、点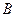 ,与直线
,与直线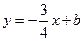 相交于点
相交于点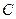 ,直线
,直线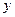 轴交于点
轴交于点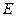 。
。
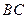 的解析式;
的解析式;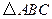 的面积;
的面积;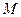 在线段
在线段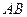 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从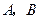 重合),同时,点
重合),同时,点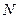 在射线
在射线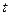 秒,请写出
秒,请写出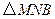 的面积
的面积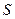 与
与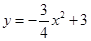 与
与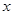 轴交于点
轴交于点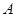 ,点
,点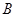 ,与直线
,与直线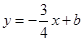 相交于点
相交于点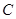 ,直线
,直线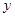 轴交于点
轴交于点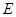 .
.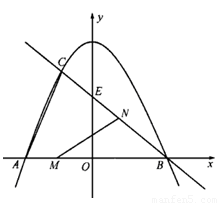
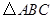 的面积.
的面积.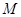 在线段
在线段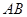 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从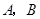 重合),同时,点
重合),同时,点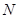 在射线
在射线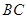 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从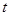 秒,请写出
秒,请写出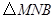 的面积
的面积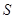 与
与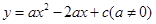 与
与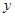 轴交于点
轴交于点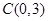 ,与
,与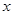 轴交于
轴交于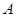 、
、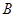 两点,点
两点,点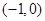 .
.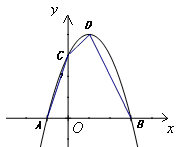
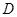 的坐标;
的坐标;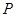 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形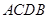 面积相等的四边形
面积相等的四边形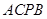 的点
的点 的面积.
的面积.