题目内容
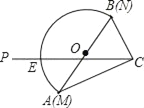
【题目】![]() 是
是![]() 的内切圆,且
的内切圆,且![]() ,切点为
,切点为![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() 的长是方程
的长是方程![]() 的两个根,则
的两个根,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
由已知的方程可求出AF、BE的长,结合切线长定理和勾股定理,可求得CE、CF的长,进而可求出AC、BC的长;根据直角三角形的面积公式即可求出其面积.
如图,解方程x2﹣13x+30=0,得:x=10,x=3,∴AD=AF=10,BD=BE=3.
设CE=CF=x,则AC=10+x,BC=3+x.
由勾股定理,得:AB2=AC2+BC2,即132=(10+x)2+(3+x)2,解得:x=2或x=-15(不合题意,舍去),∴x=2,∴AC=12,BC=5.
因此S△ABC=![]() ACBC=
ACBC=![]() ×5×12=30.
×5×12=30.
故选A.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目