题目内容
 已知:△ABC中,D为BC的中点,E为AB上一点,且BE=
已知:△ABC中,D为BC的中点,E为AB上一点,且BE= AB.F为AC上一点,且CF=
AB.F为AC上一点,且CF= AC,EF交AD于P.
AC,EF交AD于P.
(1)求EP:PF的值.
(2)求AP:PD的值.
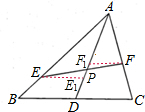
解:(1)分别作EE1,FF1平行于BC且与AD交于E1、F1两点.
则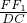 =
= =
= ,
,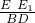 =
= =
= ,
,
又BD=CD,
∴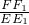 =
= ∴
∴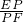 =
=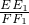 =
= ;
;
(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,
则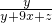 =
= ,
,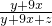 =
= ,
,
解得y=36x,z=15x,
∴ =
=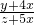 =
=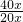 =
= .
.
分析:(1)分别作EE1,FF1平行于BC且与AD交于E1、F1两点.则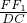 与
与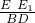 的值,根据BD=CD,则
的值,根据BD=CD,则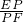 的值即可,
的值即可,
(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,得出关于x,y,z的式子,再用含有x的式子表示y,z,即可得出答案.
点评:本题考查了平行线分线段成比例定理,是基础知识比较简单.
则
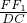 =
= =
= ,
,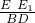 =
= =
= ,
,
又BD=CD,
∴
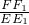 =
= ∴
∴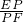 =
=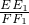 =
= ;
;(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,
则
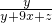 =
= ,
,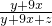 =
= ,
,解得y=36x,z=15x,
∴
 =
=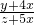 =
=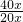 =
= .
.分析:(1)分别作EE1,FF1平行于BC且与AD交于E1、F1两点.则
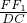 与
与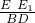 的值,根据BD=CD,则
的值,根据BD=CD,则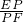 的值即可,
的值即可,(2)设AF1=y,F1P=4x,PE1=5x,E1D=z,得出关于x,y,z的式子,再用含有x的式子表示y,z,即可得出答案.
点评:本题考查了平行线分线段成比例定理,是基础知识比较简单.

练习册系列答案
相关题目
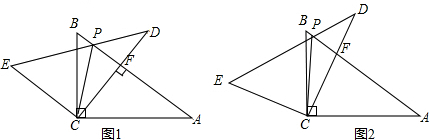
 如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示)
如图所示,已知在△ABC中,AB=AC,∠BAD=β,且AD=AE,求∠EDC.(用β表示) 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.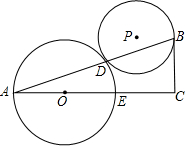 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,