题目内容
 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为xm,绿化带的面积为ym2.则y与x之间的函数关系式是
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带的BC边长为xm,绿化带的面积为ym2.则y与x之间的函数关系式是y=-
x2+20x
| 1 |
| 2 |
y=-
x2+20x
,自变量x的取值范围是| 1 |
| 2 |
0<x≤25
0<x≤25
.分析:根据矩形的面积公式列出关于二次函数解析式;根据墙长、x、y所表示的实际意义来确定x的取值范围.
解答:解:由题意得:
y=x•
=-
x2+20x,自变量x的取值范围是0<x≤25.
故答案是:y=-
x2+20x,0<x≤25.
y=x•
| 40-x |
| 2 |
| 1 |
| 2 |
故答案是:y=-
| 1 |
| 2 |
点评:本题考查了二次函数在实际生活中的应用.在求自变量x的取值范围时,要根据函数中自变量所表示的实际意义来确定.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
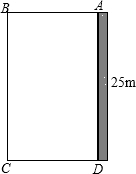 带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2.
带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.