题目内容
O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为( )

- A.8cm
- B.9cm
- C.10cm
- D.11cm
C
试题分析:由BO为∠ABC的平分线,得到一对角相等,再由OD与AB平行,根据两直线平行内错角相等得到一对角相等,等量代换得到∠DBO=∠DOB,再由等角对等边得到OD=BD,同理OE=CE,然后利用三边之和表示出三角形ODE的周长,等量代换得到其周长等于BC的长,由BC的长即可求出三角形ODE的周长.
∵BO平分∠ABC,
∴∠ABO=∠DBO,
又OD∥AB,
∴∠ABO=∠DOB,
∴∠DBO=∠DOB,
∴OD=BD,
同理OE=CE,
∵BC=10cm,
则△ODE的周长=OD+DE+OE=BD+DE+EC=BC=10cm.
考点:此题考查了等腰三角形的判定与性质,平行线的性质
点评:本题利用了等量代换的思想,熟练掌握等腰三角形的判定与性质,平行线的性质是解本题的关键.
试题分析:由BO为∠ABC的平分线,得到一对角相等,再由OD与AB平行,根据两直线平行内错角相等得到一对角相等,等量代换得到∠DBO=∠DOB,再由等角对等边得到OD=BD,同理OE=CE,然后利用三边之和表示出三角形ODE的周长,等量代换得到其周长等于BC的长,由BC的长即可求出三角形ODE的周长.
∵BO平分∠ABC,
∴∠ABO=∠DBO,
又OD∥AB,
∴∠ABO=∠DOB,
∴∠DBO=∠DOB,
∴OD=BD,
同理OE=CE,
∵BC=10cm,
则△ODE的周长=OD+DE+OE=BD+DE+EC=BC=10cm.
考点:此题考查了等腰三角形的判定与性质,平行线的性质
点评:本题利用了等量代换的思想,熟练掌握等腰三角形的判定与性质,平行线的性质是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
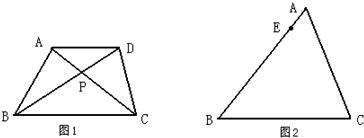
 13、如图,D是△ABC中AB边上的一点,要使△ABC∽△ACD,还应补充的条件是
13、如图,D是△ABC中AB边上的一点,要使△ABC∽△ACD,还应补充的条件是 如图,P是△ABC中AB上一点(AB>AC),则下列条件不一定能使△ACP∽△ABC的是( )
如图,P是△ABC中AB上一点(AB>AC),则下列条件不一定能使△ACP∽△ABC的是( ) (2011•鞍山)已知如图,D是△ABC中AB边上的中点,△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形,连接DE、DF.
(2011•鞍山)已知如图,D是△ABC中AB边上的中点,△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形,连接DE、DF.