Question

【题目】如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC=50°，∠ADC=30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于点E.

（1）若将图1中的线段AD沿MN向右平移到A1D1如图2所示位置，此时A1E平分∠AA1D1，CE平分∠ACD1，A1E与CE相交于E，∠PAC=50°，∠A1D1C=30°，求∠A1EC的度数.

（2）若将图1中的线段AD沿MN向左平移到A1D1如图3所示位置，其他条件与（1）相同，求此时∠A1EC的度数.

Answer 1

【答案】（1）130°；（2）40°.

【解析】

（1）直接利用角平分线的性质结合平行线的性质得出∠CAE以及∠ECA的度数，进而得出答案；

（2）直接利用角平分线的性质结合平行线的性质得出∠1和∠2的度数，进而得出答案．

解：（1）如图所示：

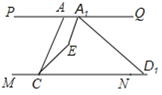
∵∠A1D1C=30°，线段AD沿MN向右平移到A1D1，PQ∥MN，

∴∠QA1D1=30°，

∴∠PA1D1=150°，

∵A1E平分∠AA1D1，

∴∠PA1E=∠EA1D1=75°，

∵∠PAC=50°，PQ∥MN，

∴∠CAQ=130°，∠ACN=50°，

∵CE平分∠ACD1，

∴∠ACE=25°，

∴∠A1EC =360°-25°-130°-75°=130°；

（2）如图所示：

过点E作FE∥PQ，

∵∠A1D1C=30°，线段AD沿MN向左平移到A1D1，PQ∥MN，

∴∠QA1D1=30°，

∵A1E平分∠AA1D1，

∴∠QA1E=∠2=15°，

∵∠PAC=50°，PQ∥MN，

∴∠ACN=50°，

∵CE平分∠ACD1，

∴∠ACE=∠ECN=∠1=25°，

∴∠A1EC =∠1+∠2=15°+25°=40°．