Question

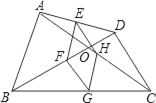
【题目】如图，在平行四边形ABCD中，E为CD上一点，连接AE，BD，且AE，BD相交于点F，DE：EC=2：3，则S△DEF：S△ABF等于（ ）

A.4:25
B.4:9
C.9:25
D.2:3

Answer 1

【答案】A
【解析】因为四边形 是平行四边形，所以AB=CD,AB//CD,所以△DEF∽△BAF,

所以 △DEF∶ △ABF= ，

因为 ∶ =2∶3，所以 ∶DC=2∶5,

所以 ∶BA=2∶5,

所以 △DEF∶ △ABF= =4∶25，故答案为：A．

由四边形 A B C D 是平行四边形，得到AB=CD，AB//CD，得到△DEF∽△BAF，根据相似三角形的面积之比等于相似比的平方，求出S△DEF：S△ABF的值.