题目内容

如图，△ABC中，∠C=90°，tan∠A=
4
5
，D为AC上一点，BC=CD=4，求△ABD的周长．
在Rt△BCD中，BC=CD=4，
根据勾股定理得：BD=
BC2+CD2
=4
2
，
在Rt△ABC中，tanA=
BC
AC
，tanA=
4
5
，
∴AC=
BC
tanA
=5，AD=AC-CD=5-4=1，
根据勾股定理得：AB=
AC2+BC2
=
41
，
则△ABD的周长为BD+AD+AB=4
2
+1+
41
．
练习册系列答案
相关题目
（1）解不等式组
x-3≤0
5(x-1)+6＞4x
并把解集在数轴上表示出来；

（2）如图，已知墙高AB为6.5米，将一长为6米的梯子CD斜靠在墙面，梯子与地面所成的角∠BCD=55°，此时梯子的顶端与墙顶的距离AD约为多少米？（结果精确到0.1米）（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）
如图，B，C是河岸边两点，A是对岸边上一点，测得∠ABC=45°，∠ACB=60°，BC=60米，甲想从A点出发在最短的时间内到达BC边，若他的速度为5米/分，则他所用的最短时间为______分．
同学们在学完解直角三角形的应用后，某合作学习小组用测倾器、皮尺测量了学校旗杆的高度，他们设计了如下方案（如图所示）：
①在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=30°；
②量出测点A到旗杆底部N的水平距离AN=20m；
③量出测倾器的高度AC=1m．
（1）根据上述测量数据，即可求出旗杆的高度MN=______．（结果可以保留根号）
（2）如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图）的方案．要求：
（ⅰ）在图中，画出你测量小山高度MN的示意图（标上适当字母）；
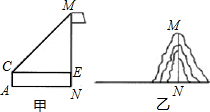（ⅱ）写出你设计的方案．（测倾器的高度用h表示，其它涉及的长度用字母a、b、c…表示，涉及到的角度用α、β…表示，最后请给出计算MN的高度的式子）．
在△ABC中，AB=AC=5，sin∠ABC=0.8，则BC=______．
已知：如图，A、B、C三个村庄在一条东西走向的公路沿线上，AB=2km．在B村的正北方向有一个D村，测得∠DAB=45°，∠DCB=28°．今将△ACD区域进行规划，除其中面积为0.5km2的水塘外，准备把剩余的一半作为绿化用地，试求绿化用地的面积．（结果精确到0.1km2，sin28°=0.4695，cos28°=0.8829，tan28°=0.5317，cot28°=1.88.8）
如图，在小山的东侧A庄有一热气球，由于受西风的影响，以每分钟35m的速度沿着与水平方向成75°的方向飞行，40min时到达C处，此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上，同时测得B庄的俯角为30°，又在A庄测得山顶P的仰角为45°．则A庄与B庄的距离为______，山高是______．（保留准确值）
如图，已知一商场自动扶梯的长l为10米，该自动扶梯到达的高度h为6米，自动扶梯与地面所成的角为θ，则tanθ的值等于（　　）
A．
3
4
B．
4
3
C．
3
5
D．
4
5
如图所示，课外活动中，小明在离旗杆AB的10米C处，用测角仪测得旗杆顶部A的仰角为40°，已知测角仪器的高CD=15米，求旗杆AB的高．（精确到0.1米）
（供选用的数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网