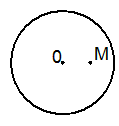题目内容

精英家教网如图，过圆O内一点M的最长的弦长为10，最短的弦长为8，求OM的长．
分析：过M的最长弦应该是⊙O的直径，最短弦应该是和OM垂直的弦（设此弦为CD）；可连接OM、OC，根据垂径定理可得出CM的长，再根据勾股定理即可求出OM的值．
解答：精英家教网解：连接OM交圆O于点B，延长MO交圆于点A，
过点M作弦CD⊥AB，连接OC
∵过圆O内一点M的最长的弦长为10，最短的弦长为8，（2分）
∴直径AB=10，CD=8
∵CD⊥AB
∴CM=MD=
1
2
CD=4（4分）
在Rt△OMC中，OC=
1
2
AB=5；
∴OM=
OC2-CM2
=3．（6分）
点评：此题考查的是垂径定理及勾股定理的应用，解答此题的关键是理解过M点的最长弦和最短弦．
练习册系列答案
相关题目
阅读下列材料后回答问题：
在平面直角坐标系中，已知x轴上的两点A（x1，0），B（x2，0）的距离记作|AB|=|x1-x2|，如果A（x1，y1），B（x2，y2）是平面上任意两点，我们可以通过构造直角三角形来求A、B间的距离．
如图，过A、B两点分别向x轴、y轴作垂线AM1、AN1和BM2、BN2，垂足分别记作M1（x1，0），N1（0，y1）、M2（x2，0），N2（0，y2），直线AN1与BM2交于Q点．
在Rt△ABQ中，|AB|2=|AQ|2+|QB|2，∵|AQ|=|M1M2|=|x2-x1|，|BQ|=|N1N2|=|y2-y1|
∴|AB|2=|x2-x1|2+|y2-y1|2由此得任意两点A（x1，y1），B（x2，y2）之间的距离公式：|AB|=
|x2-x1|2+|y2-y1|2

如果某圆的圆心为（0，0），半径为r．设P（x，y）是圆上任一点，根据“圆上任一点到定点（圆心）的距离都等于定长（半径）”，我们不难得到|PO|=r，即
(x-0)2+(y-0)2
=r，整理得：x2+y2=r2．我们称此式为圆心在精英家教网原点，半径为r的圆的方程．
（1）直接应用平面内两点间距离公式，求点A（1，-3），B（-2，1）之间的距离；
（2）如果圆心在点P（2，3），半径为3，求此圆的方程．
（3）方程x2+y2-12x+8y+36=0是否是圆的方程？如果是，求出圆心坐标与半径．
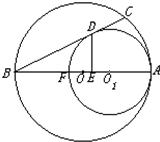25、已知：如图，⊙O和⊙O1内切于A，直线OO1交⊙O于另一点B、交⊙O1于另一点F，过B点作⊙O1的切线，切点为D，交⊙O于C点，DE⊥AB，垂足为E．求证：
（1）CD=DE；
（2）若将两圆内切改为外切，其它条件不变，（1）中的结论是否成立？请证明你的结论．
如图，过圆O内一点M的最长的弦长为10，最短的弦长为8，求OM的长。
如图，过圆O内一点M的最长的弦长为10，最短的弦长为8，求OM的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网